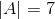Call Now to Set Up Tutoring:

(888) 888-0446

Set Theory : Cardinal numbers

Study concepts, example questions & explanations for Set Theory

Create An Account

All Set Theory Resources

7 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Cardinal Numbers

Given the set $\displaystyle A$ , calculate the cardinality.

$A=\begin{Bmatrix} 3,7,5,4,9,11,24 \end{Bmatrix}$ $\displaystyle A=\begin{Bmatrix} 3,7,5,4,9,11,24 \end{Bmatrix}$

Possible Answers:

|A|=21 $\displaystyle |A|=21$

|A|=11 $\displaystyle |A|=11$

|A|=7 $\displaystyle |A|=7$

|A|=9 $\displaystyle |A|=9$

|A|=8 $\displaystyle |A|=8$

Correct answer:

|A|=7 $\displaystyle |A|=7$

Explanation:

Given a set $\displaystyle W$ , the cardinality is the number of elements in $\displaystyle W$ . This is also written as |W| $\displaystyle |W|$ .

Looking at this particular problem,

$A=\begin{Bmatrix} 3,7,5,4,9,11,24 \end{Bmatrix}$ $\displaystyle A=\begin{Bmatrix} 3,7,5,4,9,11,24 \end{Bmatrix}$

Therefore the number of elements in a is,

|A|=7 $\displaystyle |A|=7$

Report an Error

Example Question #2 : Cardinal Numbers

Given the set $\displaystyle A$ , calculate the cardinality.

$A=\begin{Bmatrix} a,a,b,c,d,e,e \end{Bmatrix}$ $\displaystyle A=\begin{Bmatrix} a,a,b,c,d,e,e \end{Bmatrix}$

Possible Answers:

$|A|=\frac{a+e}{7}$ $\displaystyle |A|=\frac{a+e}{7}$

|A|=5 $\displaystyle |A|=5$

|A|=c $\displaystyle |A|=c$

|A|=a $\displaystyle |A|=a$

|A|=7 $\displaystyle |A|=7$

Correct answer:

|A|=5 $\displaystyle |A|=5$

Explanation:

Given a set $\displaystyle W$ , the cardinality is the number of elements in $\displaystyle W$ . This is also written as |W| $\displaystyle |W|$ .

Looking at this particular problem,

$A=\begin{Bmatrix} a,a,b,c,d,e,e \end{Bmatrix}$ $\displaystyle A=\begin{Bmatrix} a,a,b,c,d,e,e \end{Bmatrix}$

First, rewrite the set to depict a more accurate description of the space.

$A=\begin{Bmatrix} a,b,c,d,e \end{Bmatrix}$ $\displaystyle A=\begin{Bmatrix} a,b,c,d,e \end{Bmatrix}$

Therefore, counting up the number of elements, results in the following cardinality,

|A|=5 $\displaystyle |A|=5$

Report an Error

View Tutors

Agnes
Certified Tutor

Cebu Normal University, Bachelor of Science, Mathematics.

View Tutors

Danielle
Certified Tutor

Baylor University, Bachelor of Science, Health Sciences, General.

View Tutors

Tracy
Certified Tutor

Walden University, Doctor of Philosophy, Elementary School Teaching.

All Set Theory Resources

7 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Houston, Spanish Tutors in Miami, Calculus Tutors in San Francisco-Bay Area, SSAT Tutors in Miami, GRE Tutors in Washington DC, GRE Tutors in San Diego, LSAT Tutors in San Francisco-Bay Area, English Tutors in Chicago, Physics Tutors in Houston, MCAT Tutors in San Diego

Popular Courses & Classes

GRE Courses & Classes in Boston, SAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Washington DC, SAT Courses & Classes in Boston, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Boston, ACT Courses & Classes in Atlanta, LSAT Courses & Classes in San Diego, Spanish Courses & Classes in San Diego

Popular Test Prep

SSAT Test Prep in Los Angeles, MCAT Test Prep in Houston, SSAT Test Prep in Chicago, LSAT Test Prep in San Diego, SAT Test Prep in Phoenix, GRE Test Prep in New York City, GRE Test Prep in Phoenix, MCAT Test Prep in San Diego, GRE Test Prep in Boston, LSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Set Theory : Cardinal numbers

Study concepts, example questions & explanations for Set Theory

All Set Theory Resources

Example Questions

Example Question #1 : Cardinal Numbers

Example Question #2 : Cardinal Numbers

All Set Theory Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: