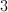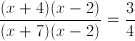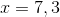All SAT Math Resources
Example Questions
Example Question #31 : Variables
Solve for 
Factor the expression
numerator: find two numbers that add to 2 and multiply to -8 [use 4,-2]
denominator: find two numbers that add to 5 and multiply to -14 [use 7,-2]
new expression:
Cancel the 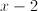
Example Question #2 : Binomials
If 〖(x+y)〗2 = 144 and 〖(x-y)〗2 = 64, what is the value of xy?
20
16
18
22
20
We first expand each binomial to get x2 + 2xy + y2 = 144 and x2 - 2xy + y2 = 64. We then subtract the second equation from the first to find 4xy = 80. Finally, we divide each side by 4 to find xy = 20.
Example Question #1 : How To Factor A Trinomial
Solve each problem and decide which is the best of the choices given.
What are the zeros of the following trinomial?
First factor out a 


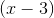
Set everything equal to zero and you get 



Example Question #2163 : Sat Mathematics
Subtract 

Step 1: We need to read the question carefully. It says subtract from. When you see the word "from", you read the question right to left.
I am subtracting the left equation from the right equation.
Step 2: We need to write the equation on the right minus the equation of the left.
Step 3: Distribute the minus sign in front of the parentheses:
Step 4: Combine like terms:
Step 5: Put all the terms together, starting with highest degree. The degree of the terms is the exponent. Here, the highest degree is 2 and lowest is zero.
The final equation is 
Example Question #1 : Variables
What is a possible value for x in x2 – 12x + 36 = 0 ?
–6
2
6
There is not enough information
6
You need to factor to find the possible values for x. You need to fill in the blanks with two numbers with a sum of -12 and a product of 36. In both sets of parenthesis, you know you will be subtracting since a negative times a negative is a positive and a negative plus a negative is a negative
(x –__)(x –__).
You should realize that 6 fits into both blanks.
You must now set each set of parenthesis equal to 0.
x – 6 = 0; x – 6 = 0
Solve both equations: x = 6
Example Question #1 : How To Factor A Polynomial
If r and t are constants and x2 +rx +6=(x+2)(x+t), what is the value of r?
It cannot be determined from the given information.
6
5
7
5
We first expand the right hand side as x2+2x+tx+2t and factor out the x terms to get x2+(2+t)x+2t. Next we set this equal to the original left hand side to get x2+rx +6=x2+(2+t)x+2t, and then we subtract x2 from each side to get rx +6=(2+t)x+2t. Since the coefficients of the x terms on each side must be equal, and the constant terms on each side must be equal, we find that r=2+t and 6=2t, so t is equal to 3 and r is equal to 5.
Example Question #2 : How To Factor A Polynomial
Solve for 
First, add 4 to both sides:
Divide both sides by 2:
Example Question #3 : How To Factor A Polynomial
Let 





Cannot be determined
We are told that x3 - y3 = 56. We can factor the left side of the equation using the formula for difference of cubes.
x3 - y3 = (x - y)(x2 + xy + y2) = 56
Since x - y = 2, we can substitute this value in for the factor x - y.
2(x2 + xy + y2) = 56
Divide both sides by 2.
x2 + xy + y2 = 28
Because we are trying to find x2 + y2, if we can get rid of xy, then we would have our answer.
We are told that 3xy = 24. If we divide both sides by 3, we see that xy = 8.
We can then substitute this value into the equation x2 + xy + y2 = 28.
x2 + 8 + y2 = 28
Subtract both sides by eight.
x2 + y2 = 20.
The answer is 20.
ALTERNATE SOLUTION:
We are told that x - y = 2 and 3xy = 24. This is a system of equations.
If we solve the first equation in terms of x, we can then substitute this into the second equation.
x - y = 2
Add y to both sides.
x = y + 2
Now we will substitute this value for x into the second equation.
3(y+2)(y) = 24
Now we can divide both sides by three.
(y+2)(y) = 8
Then we distribute.
y2 + 2y = 8
Subtract 8 from both sides.
y2 + 2y - 8 = 0
We need to factor this by thinking of two numbers that multiply to give -8 but add to give 2. These numbers are 4 and -2.
(y + 4)(y - 2) = 0
This means either y - 4 = 0, or y + 2 = 0
y = -4, or y = 2
Because x = y + 2, if y = -4, then x must be -2. Similarly, if y = 2, then x must be 4.
Let's see which combination of x and y will satisfy the final equation that we haven't used, x3 - y3 = 56.
If x = -2 and y = -4, then
(-2)3 - (-4)3 = -8 - (-64) = 56. So that means that x= -2 and y = -4 is a valid solution.
If x = 4 and y = 2, then
(4)3 - 23 = 64 - 8 = 56. So that means x = 4 and y = 2 is also a valid solution.
The final value we are asked to find is x2 + y2.
If x= -2 and y = -4, then x2 + y2 = (-2)2 + (-4)2 = 4 + 16 = 20.
If x = 4 and y = 2, then x2 + y2 = (4)2 + 22 = 16 + 4 = 20.
Thus, no matter which solution we use for x and y, x2 + y2 = 20.
The answer is 20.
Example Question #4 : How To Factor A Polynomial
How many negative solutions are there to the equation below?
First, subtract 3 from both sides in order to obtain an equation that equals 0:
The left side can be factored. We need factors of 



Set both factors equal to 0 and solve:
To solve the left equation, add 1 to both sides. To solve the right equation, subtract 3 from both sides. This yields two solutions:
Only one of these solutions is negative, so the answer is 1.
Example Question #2 : Factoring Polynomials
2x + 3y = 5a + 2b (1)
3x + 2y = 4a – b (2)
Express x2 – y2 in terms of a and b
〖–9a〗2 + 26ab +〖3b〗2) / 5
–〖9a〗2 + 27ab +〖3b〗2) / 5
(–9a2 – 28ab –3b2) / 5
–〖9a〗2 + 26ab –〖3b〗2) / 5
(–9a2 – 27ab +3b2) / 5
(–9a2 – 28ab –3b2) / 5
Add the two equations together to yield 5x + 5y = 9a + b, then factor out 5 to get 5(x + y) = 9a + b; divide both sides by 5 to get x + y = (9a + b)/5; subtract the two equations to get x - y = -a - 3b. So, x2 – y2 = (x + y)(x – y) = (9a + b)/5 (–a – 3b) = (–[(9a)]2 – 28ab – [(3b)]2)/5
Certified Tutor
All SAT Math Resources