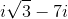We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Squaring / Square Roots / Radicals

Simplify the expression.

$\sqrt{5}(2\sqrt{3}+\sqrt{12})$

Possible Answers:

$4\sqrt{30}$

$10\sqrt{15}$

$4\sqrt{15}$

$10\sqrt{3}$

$3\sqrt{2}$

Correct answer:

$4\sqrt{15}$

Explanation:

Use the distributive property for radicals.

$\sqrt{5}(2\sqrt{3}+\sqrt{12})$

Multiply all terms by $\sqrt{5}$ .

$(\sqrt{5}*2\sqrt{3})+(\sqrt{5}*\sqrt{12})$

Combine terms under radicals.

$2\sqrt{3*5}+\sqrt{12*5}$

$2\sqrt{15}+\sqrt{60}$

Look for perfect square factors under each radical. has a perfect square of . The can be factored out.

$2\sqrt{15}+\sqrt{4*15}$

$2\sqrt{15}+2\sqrt{15}$

Since both radicals are the same, we can add them.

$4\sqrt{15}$

Report an Error

Example Question #4 : Squaring / Square Roots / Radicals

Which of the following expression is equal to

$\sqrt{(45)(9)+(27)(36)}$

Possible Answers:

$7\sqrt{15}$

$9\sqrt{17}$

$9\sqrt{15}$

$7\sqrt{17}$

$9\sqrt{19}$

Correct answer:

$9\sqrt{17}$

Explanation:

$\sqrt{(45)(9)+(27)(36)}$

When simplifying a square root, consider the factors of each of its component parts:

$\sqrt{(3^2)\times5\times(3^{2})+(3^{3})(2^2)(3^2)}$

Combine like terms:

$\sqrt{5(3^4)+(2^2)(3^5)}$

Remove the common factor, 3^4 :

$\sqrt{(3^4)\times(5+3\times(2^2))}$

Pull the $\sqrt{3^4}$ outside of the equation as 3^2 :

$(3^2)\sqrt{5+12}=9\sqrt{17}$

Report an Error

Example Question #1 : Squaring / Square Roots / Radicals

Which of the following is equal to the following expression?

$\sqrt{(16)(8)+(32)(20)}$

Possible Answers:

$2^{3}\sqrt{10}$

$2^{7}\sqrt{5}$

$2^4\sqrt{3}$

$2^{3}\sqrt{6}$

$2^{4}\sqrt{5}$

Correct answer:

$2^4\sqrt{3}$

Explanation:

$\sqrt{(16)(8)+(32)(20)}$

First, break down the components of the square root:

$\sqrt{(2^{4})(2^{3})+(2^{5})(2^{2})\times 5}$

Combine like terms. Remember, when multiplying exponents, add them together:

$\sqrt{(2^{7})+(2^{7})\times5}$

Factor out the common factor of 2^7 :

$\sqrt{(2^{7})(1+5)}$

$\sqrt{(2^7)\times6}$

Factor the :

$\sqrt{(2^7)\times2\times3}$

Combine the factored with the 2^7 :

$\sqrt{(2^{8})\times3}$

Now, you can pull $\sqrt{2^8}$ out from underneath the square root sign as 2^4 :

$2^4\sqrt{3}$

Report an Error

Example Question #6 : Squaring / Square Roots / Radicals

Which of the following expressions is equal to the following expression?

$\sqrt{(27)(45)(125)}$

Possible Answers:

$125\sqrt{27}$

$205\sqrt{3}$

$225\sqrt{3}$

$75\sqrt{20}$

$135\sqrt{5}$

Correct answer:

$225\sqrt{3}$

Explanation:

$\sqrt{(27)(45)(125)}$

First, break down the component parts of the square root:

$\sqrt{(3^{3})(5\times 3^{2})(5^{3})}$

Combine like terms in a way that will let you pull some of them out from underneath the square root symbol:

$\sqrt{(5^{4})(3^4)(3)}$

Pull out the terms with even exponents and simplify:

$(5^{2})(3^{2})\sqrt{3}=225\sqrt{3}$

Report an Error

Example Question #1 : Complex Numbers

From $\frac{3}{2} + \frac{1}{4} i$ , subtract its complex conjugate. What is the difference ?

Possible Answers:

$\frac{7}{4} + \frac{7}{4} i$

$-\frac{1}{2} i$

$\frac{1}{2} i$

Correct answer:

$\frac{1}{2} i$

Explanation:

The complex conjugate of a complex number a+bi is a - bi , so $\frac{3}{2} + \frac{1}{4} i$ has $\frac{3}{2} - \frac{1}{4} i$ as its complex conjugate. Subtract the latter from the former:

$\left (\frac{3}{2} + \frac{1}{4} i \right ) - \left ( \frac{3}{2} - \frac{1}{4} i \right )$

$= \frac{3}{2} + \frac{1}{4} i - \frac{3}{2}+ \frac{1}{4} i$

$= \frac{3}{2}- \frac{3}{2} + \frac{1}{4} i + \frac{1}{4} i$

$= \frac{1}{2} i$

Report an Error

Example Question #2 : Complex Numbers

From $17 - i \sqrt{17}$ , subtract its complex conjugate.

Possible Answers:

$2 i \sqrt{17}$

$- 2 i \sqrt{17}$

Correct answer:

$- 2 i \sqrt{17}$

Explanation:

The complex conjugate of a complex number a - bi is a+ bi . Therefore, the complex conjugate of $17 - i \sqrt{17}$ is $17 + i \sqrt{17}$ ; subtract the latter from the former by subtracting real parts and subtracting imaginary parts, as follows:

$(17 - i \sqrt{17})- (17 + i \sqrt{17})$

$= 17 - i \sqrt{17} - 17 - i \sqrt{17}$

$= 17 - 17 - i \sqrt{17} - i \sqrt{17}$

$= - 2 i \sqrt{17}$

Report an Error

Example Question #3 : Complex Numbers

From $7 + i \sqrt {7 }$ , subtract its complex conjugate.

Possible Answers:

$2i \sqrt {7 }$

$-2i \sqrt {7 }$

Correct answer:

$2i \sqrt {7 }$

Explanation:

The complex conjugate of a complex number a+ bi is a - bi . Therefore, the complex conjugate of $7 + i \sqrt {7 }$ is $7 - i \sqrt {7 }$ ; subtract the latter from the former by subtracting real parts and subtracting imaginary parts, as follows:

$(7 + i \sqrt {7 })- (7 - i \sqrt {7 })$

$= 7- 7 + i \sqrt {7 }- (- i \sqrt {7 })$

$= i \sqrt {7 }+ i \sqrt {7 }$

$=2i \sqrt {7 }$

Report an Error

Example Question #4 : Complex Numbers

Simplify: $\sqrt{-3}+\sqrt{-9}+\sqrt{-16}$

Possible Answers:

$i\sqrt3 -7i$

$i\sqrt3 +i$

$i\sqrt3 +7i$

$2i\sqrt7$

$i\sqrt3-i$

Correct answer:

$i\sqrt3 +7i$

Explanation:

Rewrite $\sqrt{-3}+\sqrt{-9}+\sqrt{-16}$ in their imaginary terms.

$i=\sqrt{-1}$

$\sqrt{-3}+\sqrt{-9}+\sqrt{-16}=i\sqrt3+3i+4i = i\sqrt3 +7i$

Report an Error

Example Question #5 : Complex Numbers

Add $5 + i \sqrt {5 }$ and its complex conjugate.

Possible Answers:

$2 i \sqrt{5}$

$-2 i \sqrt{5}$

Correct answer:

Explanation:

The complex conjugate of a complex number a+ bi is a - bi . Therefore, the complex conjugate of $5 + i \sqrt {5 }$ is $5 - i \sqrt {5 }$ ; add them by adding real parts and adding imaginary parts, as follows:

$(5 + i \sqrt {5 } )+( 5 - i \sqrt {5 })$

$= 5 + 5 + i \sqrt {5 } - i \sqrt {5 }$

= 10 ,

the correct response.

Report an Error

Example Question #3 : Complex Numbers

Add $13 - i \sqrt{13}$ to its complex conjugate.

Possible Answers:

$2i \sqrt{13}$

$-2i \sqrt{13}$

Correct answer:

Explanation:

The complex conjugate of a complex number a - bi is a+ bi . Therefore, the complex conjugate of $13 - i \sqrt{13}$ is $13 + i \sqrt{13}$ ; add them by adding real parts and adding imaginary parts, as follows:

$(13 - i \sqrt{13} )+( 13 + i \sqrt{13})$

$= 13+13 - i \sqrt {13 }+ i \sqrt {13}$

= 26

Report an Error

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Kayla
Certified Tutor

University of Minnesota, Bachelor of Science, Mathematics. Boston University, Master of Arts Teaching, Mathematics Teaching.

View SAT Mathematics Tutors

Thomas
Certified Tutor

Michigan State University, Bachelor in Arts, History. Central Michigan University, Doctor of Philosophy, History.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Washington DC, GRE Courses & Classes in Washington DC, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in San Diego, LSAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Philadelphia, ISEE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in New York City

Popular Test Prep

SAT Test Prep in San Diego, MCAT Test Prep in Boston, GMAT Test Prep in Philadelphia, SSAT Test Prep in Denver, GMAT Test Prep in Washington DC, GRE Test Prep in Chicago, SAT Test Prep in Philadelphia, SSAT Test Prep in New York City, LSAT Test Prep in Washington DC, LSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #3 : Squaring / Square Roots / Radicals

Example Question #4 : Squaring / Square Roots / Radicals

Example Question #1 : Squaring / Square Roots / Radicals

Example Question #6 : Squaring / Square Roots / Radicals

Example Question #1 : Complex Numbers

Example Question #2 : Complex Numbers

Example Question #3 : Complex Numbers

Example Question #4 : Complex Numbers

Example Question #5 : Complex Numbers

Example Question #3 : Complex Numbers

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: