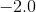A number in scientific notation takes the form , where  and is an integer.

To convert 3,880,000,000,000 to scientific notation, place the implied decimal point after the final zero and move it to the left as many places as is necessary until it is after the first nonzero digit - in this case the "3". Note that the point is moved 12 places to the left.

The number in front is 3.88, the number formed. The exponent of 10 is 12 - positive since the point was moved to the left. Therefore, the number, in scientific notation, is .

A number in scientific notation takes the form , where  and is an integer.  

An easy way to add these numbers is to note that if  and  are both positive integers,  is the number  followed by  zeroes. Therefore, 

Add these numbers:

Since all four choices can be rewritten as 6 followed by a number of zeroes, none of them are equal to this sum. 

A number in scientific notation takes the form , where  and is an integer.

To multiply two numbers that are in scientific notation, first, use commutativity to multiply the numbers:

Applying the Product of Powers Rule on the powers of 10:

However, since , this number is not in scientific notation. Adjust by noting that , then applying the Product of Powers Rule again:

When written in scientific notation, a number will follow the format in which is between one and ten and is an integer value.

To find , take the first non-zero digit in your given number as the ones place. In 0.0004640 this would be the first 4. All subsequent digits fall into the tenths, hundredths, etc. places.

To find , we must count the number of places that is removed. In 0.0004640, the first digit of  is in the ten-thousandths place. This indicates that will be .

Together, the final scientific notation will be .

Add what he can purchase to what he has left over:

Two comic books and the candy bar: $1.50 + $1.0 + $0.75 = $3.75

Three quarters and two dimes: $0.75 + $0.20 = $0.95

Therefore his total amount of money is $3.75 + $0.95 = $4.70.

In order to add the decimals, add placeholders to the decimal .

Be careful not to add the wrong digits!

Add the thousandths places.

Add the hundredths places.

Add the tenths places.

Combine the numbers and put a decimal before the tenths place.

The correct answer is:  

Each route includes one path from Point A to Point B and one path from Point B o Point C.

The shortest possible drive is the sum of the shortest paths for each leg of the trip:

The longest possible drive is the sum of the longest paths for each leg of the trip:

The correct response is that .

The family's trip will be designed so that the family will take two different routes of the three that connect Town A and Town B, and two different routes of the three that connect Town B and Town C. 

The minimum distance that the family will travel is therefore the sum of the lengths of the two shortest routes from Town A to Town B, and those of the two shortest routes from Town B to Town C:

 miles

The maximum distance that the family will travel is, similarly, the sum of the lengths of the two longest routes from Town A to Town B, and those of the two longest routes from Town B to Town C:

 miles

The correct choice is therefore .

There are three routes from Point A to Point B, and three from Point B to Point C, for a total of  routes total. The total distance traveled is the distance of one of the first three routes added to that of one of the last three; we can take all nine possibilities and add the distances:

Five of these routes require driving a distance 40 miles or fewer.

0.57 - 2.657 = -2.087

Don't forget the negative sign!

This number then rounds to -2.1.