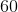All SAT Math Resources
Example Questions
Example Question #11 : Least Common Multiple
What is the least common multiple of 
We need to ensure that all the numbers share a common factor of 









Example Question #12 : Factors / Multiples
What is the least common multiple of 
We need to ensure that all the numbers share a common factor of 














Example Question #11 : Least Common Multiple
What is the least common multiple of the first six positive integers?
Let's divide the even numbers first. We will divide them by 

Next, we have two 







Example Question #713 : Arithmetic
Which can be a group of remainders when four consecutive integers are divided by 
If you divide a number by 


Example Question #11 : Least Common Multiple
If a, b, and c are positive integers such that 4a = 6b = 11c, then what is the smallest possible value of a + b + c?
132
11
33
121
67
67
We are told that a, b, and c are integers, and that 4a = 6b = 11c. Because a, b, and c are positive integers, this means that 4a represents all of the multiples of 4, 6b represents the multiples of 6, and 11c represents the multiples of 11. Essentially, we will need to find the least common multiples (LCM) of 4, 6, and 11, so that 4a, 6b, and 11c are all equal to one another.
First, let's find the LCM of 4 and 6. We can list the multiples of each, and determine the smallest multiple they have in common. The multiples of 4 and 6 are as follows:
4: 4, 8, 12, 16, 20, ...
6: 6, 12, 18, 24, 30, ...
The smallest multiple that 4 and 6 have in common is 12. Thus, the LCM of 4 and 6 is 12.
We must now find the LCM of 12 and 11, because we know that any multiple of 12 will also be a multiple of 4 and 6.
Let's list the first several multiples of 12 and 11:
12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, ...
11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, ...
The LCM of 12 and 11 is 132.
Thus, the LCM of 4, 6, and 12 is 132.
Now, we need to find the values of a, b, and c, such that 4a = 6b = 12c = 132.
4a = 132
Divide each side by 4.
a = 33
Next, let 6b = 132.
6b = 132
Divide both sides by 6.
b = 22
Finally, let 11c = 132.
11c = 132
Divide both sides by 11.
c = 12.
Thus, a = 33, b = 22, and c = 12.
We are asked to find the value of a + b + c.
33 + 22 + 12 = 67.
The answer is 67.
Example Question #1 : How To Find The Greatest Common Factor
If 
Since v is divisible by 2, 3 and 15, v must be a multiple of 30. Any number that is divisible by both 2 and 15 must be divisible by their product, 30, since this is the least common multiple.
Out of all the answer choices, v + 30 is the only one that equals a multiple of 30.
Example Question #2 : How To Find The Greatest Common Factor
Suppose that 



We are given information that m/4 is 10 greater than m/3. We set up an equation where m/4 = m/3 + 10.
We must then give the m variables a common denominator in order to solve for m. Since 3 * 4 = 12, we can use 12 as our denominator for both m variables.
m/4 = m/3 + 10 (Multiply m/4 by 3 in the numerator and denominator.)
3m/12 = m/3 + 10 (Multiply m/3 by 4 in the numerator and denominator.)
3m/12 = 4m/12 + 10 (Subtract 4m/12 on both sides.)
-m/12 = 10 (Multiply both sides by -12.)
m = -120
-120/4 = -30 and -120/3 = -40. -30 is 10 greater than -40.
Example Question #3 : Factors / Multiples



The greatest common divisor of 

The greatest common divisor of 

The greatest common divisor of 

If 
The greatest common divisor of 



The greatest common divisor of 



The greatest common divisor of 



Thus:
We substitute these equalities into the given expression and simplify.
Since 










Therefore:
or
Example Question #1 : Greatest Common Factor
What's the greatest common factor of 6 and 8?
Greatest common factor is a common factor shared by two or more numbers. Both numbers are even, so let's divide both numbers by two. We get 

Example Question #5 : How To Find The Greatest Common Factor
What's the greatest common factor of 4 and 8?
Greatest common factor is a common factor shared by two or more numbers. 




Certified Tutor
All SAT Math Resources