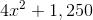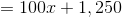All SAT Math Resources
Example Questions
Example Question #1 : How To Find The Surface Area Of A Prism

The shaded face of the above rectangular prism is a square. In terms of 
Since the front face of the prism is a square, the common sidelength - and the missing dimension - is 
There are two faces (front and back) that are squares of sidelength 

There are four faces (left, right, top, bottom) that are rectangles of dimensions 25 and 

The surface area is the total of their areas:
Example Question #21 : Prisms
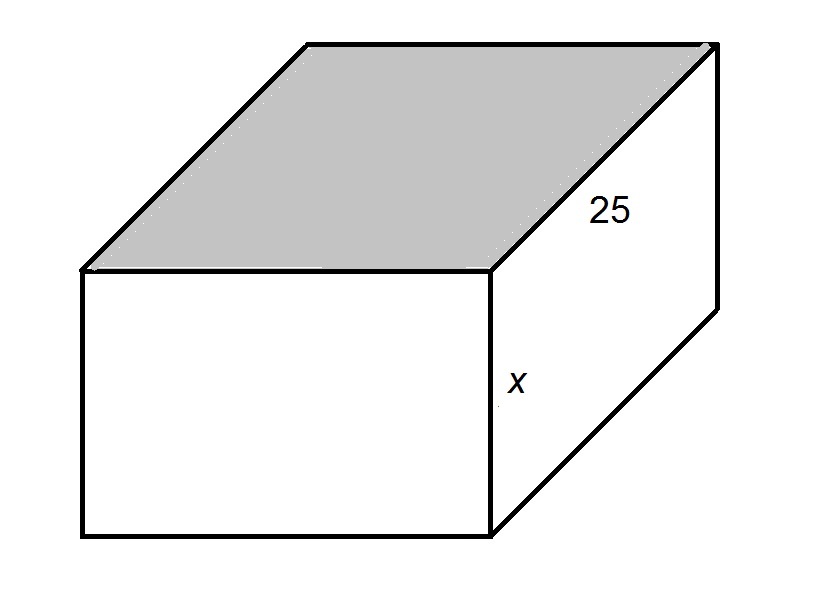
The shaded face of the above rectangular prism is a square. In terms of 
Since the top face of the prism is a square, the common sidelength - and the missing dimension - is 25.
The surface area 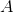




Setting

Example Question #1 : How To Find The Volume Of A Prism
A rectangular box has a length of 2 meters, a width of 0.5 meters, and a height of 3.2 meters. How many cubes with a volume of one cubic centimeter could fit into this rectangular box?
3,2 x 103
3.2 x 106
3.2
3.2 x 102
3.2 x 10-3
3.2 x 106
In order to figure out how many cubic centimeters can fit into the box, we need to figure out the volume of the box in terms of cubic centimeters. However, the measurements of the box are given in meters. Therefore, we need to convert these measurements to centimeters and then determine the volume of the box.
There are 100 centimeters in one meter. This means that in order to convert from meters to centimeters, we must multiply by 100.
The length of the box is 2 meters, which is equal to 2 x 100, or 200, centimeters.
The width of the box is 0.5(100) = 50 centimeters.
The height of the box is 3.2(100) = 320 centimeters.
Now that all of our measurements are in centimeters, we can calculate the volume of the box in cubic centimeters. Remember that the volume of a rectangular box (or prism) is equal to the product of the length, width, and height.
V = length x width x height
V = (200 cm)(50 cm)(320 cm) = 3,200,000 cm3
To rewrite this in scientific notation, we must move the decimal six places to the left.
V = 3.2 x 106 cm3
The answer is 3.2 x 106.
Example Question #1 : How To Find The Volume Of A Prism
A rectangular prism has a length that is twice as long as its width, and a width that is twice as long as its height. If the surface area of the prism is 252 square units, what is the volume, in cubic units, of the prism?
432
216
27
1728
108
216
Let l be the length, w be the width, and h be the height of the prism. We are told that the length is twice the width, and that the width is twice the height. We can set up the following two equations:
l = 2w
w = 2h
Next, we are told that the surface area is equal to 252 square units. Using the formula for the surface area of the rectangular prism, we can write the following equation:
surface area = 2lw + 2lh + 2wh = 252
We now have three equations and three unknowns. In order to solve for one of the variables, let's try to write w and l in terms of h. We know that w = 2h. Because l = 2w, we can write l as follows:
l = 2w = 2(2h) = 4h
Now, let's substitute w = 2h and l = 4h into the equation we wrote for surface area.
2(4h)(2h) + 2(4h)(h) + 2(2h)(h) = 252
Simplify each term.
16h2 + 8h2 + 4h2 = 252
Combine h2 terms.
28h2 = 252
Divide both sides by 28.
h2 = 9
Take the square root of both sides.
h = 3.
This means that h = 3. Because w = 2h, the width must be 6. And because l = 2w, the length must be 12.
Because we now know the length, width, and height, we can find the volume of the prism, which is what the question ultimately requires us to find.
volume of a prism = l • w • h
volume = 12(6)(3)
= 216 cubic units
The answer is 216.
Example Question #91 : Geometry
The dimensions of Treasure Chest A are 39” x 18”. The dimensions of Treasure Chest B are 16” x 45”. Both are 11” high. Which of the following statements is correct?
Treasure Chest A has the same surface area as Treasure Chest B.
Treasure Chest B can hold more treasure.
There is insufficient data to make a comparison between Treasure Chest A and Treasure Chest B.
Treasure Chest A can hold more treasure.
Treasure Chest A and B can hold the same amount of treasure.
Treasure Chest B can hold more treasure.
The volume of B is 7920 in3. The volume of A is 7722 in3. Treasure Chest B can hold more treasure.
Example Question #81 : Solid Geometry
Carlos has a pool in the shape of a rectangular prism. He fills the pool with a hose that ejects water at a rate of p gallons per minute. The bottom of the pool is A meters wide and B meters long. If there are k gallons in a cubic meter, then which of the following expressions will be equal to the amount of time it takes, in hours, for the water in the pool to reach a height of c meters?
ABcp/(60k)
60ABcp/k
ABck/(60p)
ABc/(pk)
60ABc/(pk)
ABck/(60p)
Example Question #776 : Sat Mathematics
A given cube with a volume of 
The question tells us that the cube is split into two prisms of equal size. Therefore, we don't even need to use the formula for the volume of a prism. If the cube is split into two equal forms, then the two prisms will be equal to one-half of the cube's volume.
Example Question #81 : Solid Geometry
A cube with volume 27 cubic inches is inscribed inside a sphere such that each vertex of the cube touches the sphere. What is the radius, in inches, of the sphere?
(3√3)/2 (approximately 2.60)
8.5
√3/2 (approximately 1.73)
9
(3√3)/2 (approximately 2.60)
We know that the cube has a volume of 27 cubic inches, so each side of the cube must be ∛27=3 inches. Since the cube is inscribed inside the sphere, the diameter of the sphere is the diagonal length of the cube, so the radius of the sphere is half of the diagonal length of the cube. To find the diagonal length of the cube, we use the distance formula d=√(32+32+32 )=√(3*32 )=3√3, and then divide the result by 2 to find the radius of the sphere, (3√3)/2.
Example Question #1 : Spheres
The surface area of a sphere is 100π square feet. What is the radius in feet?
5
π
100
10
25
5
S = 4π(r2)
100π = 4π(r2)
100 = 4r2
25 = r2
5 = r
Example Question #3 : Spheres
What is the radius of a sphere with a surface area of 16?
In order to find the radius, first write the surface area formula for a sphere and substitute the surface area.
Divide by 

Simplify both sides of the equation.
Square root both sides.
The radius is 
Certified Tutor
All SAT Math Resources