SAT Math : Geometry
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #61 : Geometry
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
45m
25m
30m
40m
35m
25m
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
Example Question #51 : Triangles
Paul leaves his home and jogs 3 miles due north and 4 miles due west. If Paul could walk a straight line from his current position back to his house, how far, in miles, is Paul from home?
25
7
4
5
√14
5
By using the Pythagorean Theorem, we can solve for the distance “as the crow flies” from Paul to his home:
32 + 42 = x2
9 + 16 = x2
25 = x2
5 = x
Example Question #52 : Triangles
Given a right triangle where the two legs have lengths of 3 and 4 respectively, what is the length of the hypotenuse?
5
3
4
9
25
5
The hypotenuse can be found using Pythagorean Theorem, which is a2 + b2 = c2, so we plug in a = 3 and b = 4 to get c.
c2 =25, so c = 5
Example Question #62 : Geometry
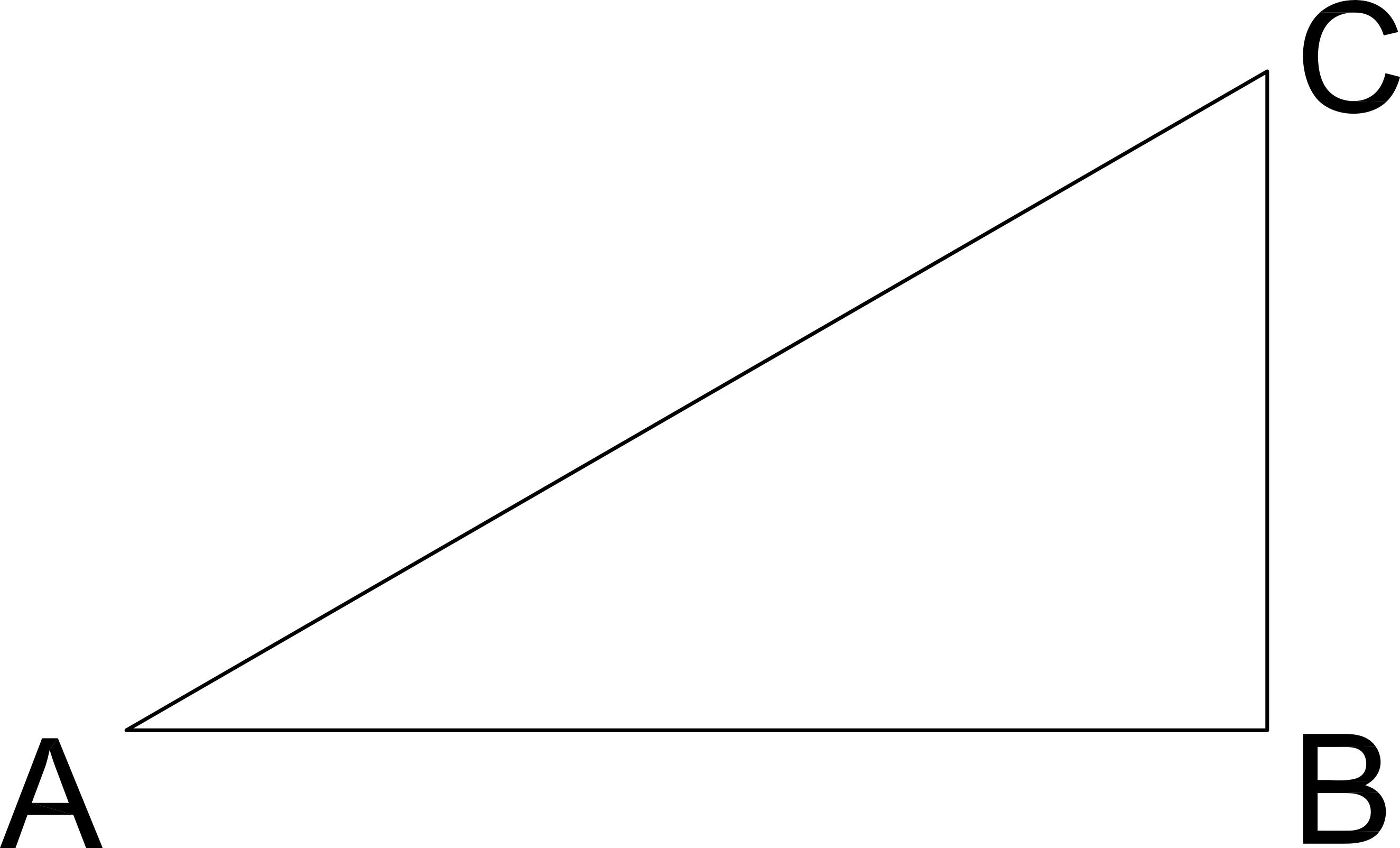
Length AB = 4
Length BC = 3
If a similar triangle has a hypotenuse length of 25, what are the lengths of its two legs?
20 and 25
5 and 25
3 and 4
15 and 25
15 and 20
15 and 20
Similar triangles are in proportion.
Use Pythagorean Theorem to solve for AC:
Pythagorean Theorem: AB2 + BC2 = AC2
42 + 32 = AC2
16 + 9 = AC2
25 = AC2
AC = 5
If the similar triangle's hypotenuse is 25, then the proportion of the sides is AC/25 or 5/25 or 1/5.
Two legs then are 5 times longer than AB or BC:
5 * (AB) = 5 * (4) = 20
5 * (BC) = 5 * (3) = 15
Example Question #61 : Sat Mathematics
If the base of a right triangle is 5 cm long and the height of the triangle is 7 cm longer than the base, what is the length of the third side of the triangle in cm?
Find the height of the triangle
Use the Pythagorean Theorem to solve for the length of the third side, or hypotenuse.
Example Question #21 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Given the right triangle in the diagram, what is the length of the hypotenuse?
To find the length of the hypotenuse use the Pythagorean Theorem:
Where 
The hypotenuse is 10 inches long.
Example Question #61 : Geometry
Triangle ABC is a right triangle. If the length of side A = 3 inches and C = 5 inches, what is the length of side B?
4.5 inches
4 inches
6 inches
1/2 inches
1 inches
4 inches
Using the Pythagorean Theorem, we know that 
This gives:
Subtracting 9 from both sides of the equation gives:
Example Question #41 : Triangles
Triangle ABC is a right triangle. If the length of side A = 8 inches and B = 11 inches, find the length of the hypoteneuse (to the nearest tenth).
13.7 inches
13.6 inches
14.2 inches
185 inches
184 inches
13.6 inches
Using the Pythagrean Theorem, we know that 
This tells us:
Taking the square root of both sides, we find that 
Example Question #21 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Given:
A = 6 feet
B = 9 feet
What is the length of the hypoteneuse of the triangle (to the nearest tenth)?
10.6 feet
10.2 feet
10.8 feet
10.1 feet
10.5 feet
10.8 feet
Using the Pythagrean Theorem, we know that 
This tells us:
Taking the square root of both sides, we find that
Example Question #62 : Sat Mathematics
Given:
A = 2 miles
B = 3 miles
What is the length of the hypoteneuse of triangle ABC, to the nearest tenth?
3.6 miles
3.2 miles
3.5 miles
3.7 miles
3.4 miles
3.6 miles
Using the Pythagrean Theorem, we know that 
This tells us:
Taking the square root of both sides, we find that
Certified Tutor
All SAT Math Resources
