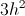All SAT Math Resources
Example Questions
Example Question #141 : Geometry
Which of the following measurements can NOT represent the sides of a triangle.
Given the Triangle Inequality, the sum of any two sides of a triangle must be greater than the third side.
Given the measurements 
Therefore, these lengths cannot represent a triangle.
Example Question #1 : How To Find The Area Of An Acute / Obtuse Triangle
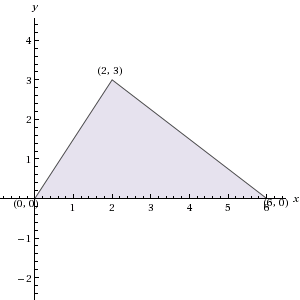
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
10
18
12
20
9
Example Question #341 : Geometry
The height, 



If 


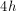
Using the formula for the area of a triangle (


Example Question #141 : Geometry
Find the height of a triangle if the area of the triangle = 18 and the base = 4.
6
1
9
4
9
The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.
Example Question #251 : Plane Geometry


The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 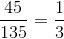
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

Example Question #33 : Acute / Obtuse Triangles
A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?
4
6
7
9
15
4
The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.
Example Question #2 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle
Two sides of a triangle are 20 and 32. Which of the following CANNOT be the third side of this triangle.
20
10
15
17
13
10
Please remember the Triangle Inequality Theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Therefore, the correct answer is 10 because the sum of 10 and 20 would not be greater than the third side 32.
Example Question #141 : Plane Geometry
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
11
5
3
7
13
13
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
Example Question #145 : Plane Geometry
The lengths of two sides of a triangle are 9 and 7. Which of the following could be the length of the third side?
12
1
16
2
17
12
Let us call the third side x. According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be larger than the other two sides. Thus, all of the following must be true:
x + 7 > 9
x + 9 > 7
7 + 9 > x
We can solve these three inequalities to determine the possible values of x.
x + 7 > 9
Subtract 7 from both sides.
x > 2
Now, we can look at x + 9 > 7. Subtracting 9 from both sides, we obtain
x > –2
Finally, 7 + 9 > x, which means that 16 > x.
Therefore, x must be greater than 2, greater than –2, but also less than 16. The only number that satisfies all of these requirements is 12.
The answer is 12.
Example Question #242 : Plane Geometry
The lengths of a triangle are 8, 12, and x. Which of the following inequalities shows all of the possible values of x?
4 ≤ x ≤12
4 < x <12
4 ≤ x ≤ 20
4 < x < 20
8 < x < 12
4 < x < 20
According to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater (not greater than or equal) than the remaining side. Thus, the following inequalities must all be true:
x + 8 > 12
x + 12 > 8
8 + 12 > x
Let's solve each inequality.
x + 8 > 12
Subtract 8 from both sides.
x > 4
Next, let's look at the inequality x + 12 > 8
x + 12 > 8
Subtract 12 from both sides.
x > –4
Lastly, 8 + 12 > x, which means that x < 20.
This means that x must be less than twenty, but greater than 4 and greater than –4. Since any number greater than 4 is also greater than –4, we can exclude the inequality x > –4.
To summarize, x must be greater than 4 and less than 20. We can write this as 4 < x < 20.
The answer is 4 < x < 20.
Certified Tutor
All SAT Math Resources