All SAT Math Resources
Example Questions
Example Question #5 : Prisms
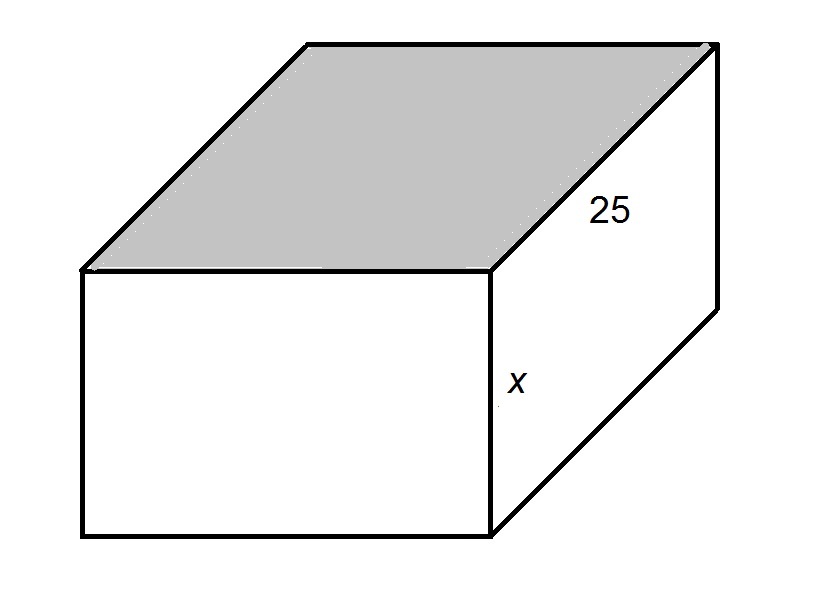
The shaded face of the above rectangular prism is a square. If the volume of the prism is 


Since the top face of the prism is a square, the common sidelength - and the missing dimension - is 25.
The volume of a rectangular prism is equal to the product of its length, width, and height - that is,
Setting 

Example Question #1 : How To Find The Diagonal Of A Prism
The dimensions of a right, rectangular prism are 4 in x 12 in x 2 ft. What is the diagonal distance of the prism?
4√(46)
8√(23)
4√(3)
None of the other answers
8√(7)
4√(46)
The problem is simple, but be careful. The units are not equal. First convert the last dimension into inches. There are 12 inches per foot. Therefore, the prism's dimensions really are: 4 in x 12 in x 24 in.
From this point, things are relatively easy. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, d2 = x2 + y2 + z2, or d = √(x2 + y2 + z2)
For our data, this would be:
d = √(42 + 122 + 242) = √(16 + 144 + 576) = √(736) = √(2 * 2 * 2 * 2 * 2 * 23) = 4√(46)
Example Question #3 : Prisms
The base of a right, rectangular prism is a square. Its height is three times that of one of the sides of the base. If its overall volume is 375 in3, what is the diagonal distance of the prism?
25√(11) in
5√(11) in
5√(3) in
None of the other answers
5 in
5√(11) in
First, let's represent our dimensions. We know the bottom could be represented as being x by x. The height is said to be three times one of these dimensions, so let's call it 3x. Based on this, we know the dimensions of the prism are x, x, and 3x. Now, the volume of a right rectangular prism is found by multiplying together its three dimensions. Therefore, if we know the overall volume is 375 in3, we can say:
375 = x * x * 3x or 375 = 3x3
Simplifying, we first divide by 3: 125 = x3. Taking the cube root of both sides, we find that x = 5.
Now, be careful. The dimensions are not 5, 5, 5. They are (recall) x, x, and 3x. If x = 5, this means the dimensions are 5, 5, and 15.
At this point, things are beginning to progress to the end of the problem. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, d2 = x2 + y2 + z2, or d = √(x2 + y2 + z2)
For our data, this would be: d = √(52 + 52 + 152) = √(25 + 25 + 225) = √(275) = √(5 * 5 * 11) = 5√(11) in
Example Question #1 : Prisms
The base of a right, rectangular prism has one side that is three times the length of the other. Its height is twice the length of the longer side of the base. If its overall volume is 13,122 in3, what is the diagonal distance of the prism?
9√(13) in
9√(23) in
None of the other answers
6√(23) in
9√(46) in
9√(46) in
First, let's represent our dimensions. We know the bottom could be represented as being x by 3x. The height is said to be twice the longer dimension, so let's call it 2 * 3x, or 6x. Based on this, we know the dimensions of the prism are x, 2x, and 6x. Now, the volume of a right rectangular prism is found by multiplying together its three dimensions. Therefore, if we know the overall volume is 13,122 in3, we can say:
13,122 = x * 3x * 6x or 13,122 = 18x3
Simplifying, we first divide by 18: 729 = x3. Taking the cube root of both sides, we find that x = 9.
Now, be careful. The dimensions are not 9, 9, and 9. They are (recall) x, 3x, and 6x. If x = 9, this means the dimensions are 9, 27, and 54.
At this point, things are beginning to progress to the end of the problem. The distance from corner to corner in a three-dimensional prism like this can be found by using a variation on the Pythagorean Theorem that merely adds one dimension. That is, d2 = x2 + y2 + z2, or d = √(x2 + y2 + z2)
For our data, this would be: d = √(92 + 272 + 542) = √(81 + 729 + 2916) = √(3726) = √(2 * 3 * 3 * 3 * 3 * 23) = 9√(46) in.
Example Question #1 : Prisms
A rectangular prism has length 7, width 4, and height 4. What is the distance from the top back left corner to the bottom front right corner?
The diagonal from the top back left corner to the bottom front right corner will be the hypotenuse of a right triangle. The sides of the triangle will be the height of the box and the diagonal through the middle of one of the rectangular faces. We will be able to solve for the length using the Pythagorean Theorem.
To calculate the length of the hypotenuse, we first must find the length of the rectangular diagonal using the sides of the rectangle. This diagonal will be the hypotenuse of a right triangle with sides 7 and 4. Solve for the diagonal length using the Pythagorean Theorem.
Now we can return to our first triangle. We are given the height, 4, and now have the length of the rectangular diagonal. Use these values to solve for the length of the diagonal that connects the top back left corner and the bottom front right corner.
Example Question #761 : Geometry

The above figure depicts a rectangular prism. Give the length of the shortest path from Point A to Point B that lies completely along the surface of the prism.
The shortest path is along two of the surfaces of the prism. There are three possibilities, each of which are shown below with the relevant faces folded out.

The top diagram shows a path along the right and the front. The path is equal in length to that of a diagonal of a rectangle of length and height 12 and 30, so the length of the path can be calculated using the Pythagorean Theorem. Setting 
The bottom diagrams show a path along the top and the front and a path along the rear and the bottom. In both cases, the path is equal in length to that of a diagonal of a rectangle of length and height 20 and 22, so the length of the path can be calculated using the Pythagorean Theorem. Setting 

The shortest distance between Points A and B along the surface is therefore 

Example Question #11 : Prisms
A rectangular prism has a volume of 70 m3. If the length, width, and height of the prism are integers measured in meters, which of the following is NOT a possible measure of the surface area of the prism measured in square meters?
118
174
214
178
280
280
Since the volume is the product of length, width, and height, and each of these three dimensions are integers, it is important to know the factors of the volume. 70 = (2)(5)(7). This implies that each of these factors (and only these factors with the exception of 1) will show up in the three dimensions exactly once. This creates precisely the following five possibilities:
2, 5, 7
SA = 2((2)(5)+(2)(7)+(5)(7)) = 118
1, 7, 10
SA = 2((1)(7)+(1)(10)+(7)(10)) = 174
1, 5, 14
SA = 2((1)(5)+(1)(14)+(5)(14)) = 178
1, 2, 35
SA = 2((1)(2)+(1)(35)+(2)(35)) = 214
1, 1, 70
SA = 2((1)(1)+(1)(70)+(1)(70)) = 282
Example Question #1 : How To Find The Surface Area Of A Prism
The three sides of a rectangular box all have integer unit lengths. If each of the side lengths is greater than one unit, and if the volume of the box is 182 cubic units, what is the surface area of the box in square units?
182
264
236
262
181
262
Let's call the side lengths of the box l, w, and h. We are told that l, w, and h must all be integer lengths greater than one. We are also told that the volume of the box is 182 cubic units.
Since the volume of a rectangular box is the product of its side lengths, this means that lwh must equal 182.
(l)(w)(h) = 182.
In order to determine possible values of l, w, and h, it would help us to figure out the factors of 182. We want to express 182 as a product of three integers each greater than 1.
Let's factor 182. Because 182 is even, it is divisible by 2.
182 = 2(91).
91 is equal to the product of 7 and 13.
Thus, 182 = 2(7)(13).
This means that the lengths of the box must be 2, 7, and 13 units.
In order to find the surface area, we can use the following formula:
surface area = 2lw + 2lh + 2hw.
surface area = 2(2)(7) + 2(2)(13) + 2(7)(13)
= 28 + 52 + 182
= 262 square units.
The answer is 262.
Example Question #11 : Prisms
A right rectangular prism has dimensions of 3 x 5 x 20. What is its surface area?
112
175
300
56
350
350
There are six faces to a right, rectangular prism. Based on our dimensions, we know that we must have a face that is 3 x 5, a face that is 5 x 20 and a face that is 3 x 20. To think this through, imagine that the front face is 3 x 5, the right side is 5 x 20, and the top is 3 x 20. Now, each of these sides has a matching side opposite (the left has the right, the top has the bottom, the front has the back).
Therefore, we know we have the following areas for the faces of our prism:
2 * 3 * 5 = 30
2 * 5 * 20 = 200
2 * 3 * 20 = 120
Add these to get the total surface area:
30 + 200 + 120 = 350
Example Question #1 : How To Find The Surface Area Of A Prism
A right rectangular prism has dimensions of 12.4 x 2.3 x 33. What is its surface area?
1027.24
1882.32
513.62
941.16
470.58
1027.24
There are six faces to a right, rectangular prism. Based on our dimensions, we know that we must have a face that is 12.4 x 2.3, a face that is 2.3 x 33 and a face that is 33 x 12.4. To think this through, imagine that the front face is 12.4 x 2.3, the left side is 2.3 x 33, and the top is 33 x 12.4. Now, each of these sides has a matching side opposite (the left has the right, the top has the bottom, the front has the back).
Therefore, we know we have the following areas for the faces of our prism:
2 * 12.4 * 2.3 = 57.04
2 * 2.3 * 33 = 151.8
2 * 12.4 * 33 = 818.4
Add these to get the total surface area:
57.04 + 151.8 + 818.4 = 1027.24
Certified Tutor
Certified Tutor
All SAT Math Resources






































