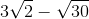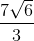We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Square Roots and Operations

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Multiply Square Roots

Simplify:

$\sqrt{3}(\sqrt{3}+4)$

Possible Answers:

$3+4\sqrt{3}$

$3+2\sqrt{3}$

$7\sqrt{3}$

$9+4\sqrt{3}$

Correct answer:

$3+4\sqrt{3}$

Explanation:

To simplify the problem, just distribute the radical to each term in the parentheses.

$\\\sqrt{3}(\sqrt{3}+4)\\=\sqrt{9}+4\sqrt{3}\\=3+4\sqrt{3}$

Report an Error

Example Question #12 : How To Multiply Square Roots

Simplify:

$\sqrt{3}(\sqrt{7}+\sqrt{12})$

Possible Answers:

$21+3\sqrt{3}$

$\sqrt{21}+3\sqrt{3}$

$\sqrt{21}+2\sqrt{2}$

$\sqrt{21}+6$

$12+4\sqrt{3}$

Correct answer:

$\sqrt{21}+6$

Explanation:

To simplify the problem, just distribute the radical to each term in the parentheses.

$\\\sqrt{3}(\sqrt{7}+\sqrt{12})\\=\sqrt{21}+\sqrt{36}\\=\sqrt{21}+6$

Report an Error

Example Question #13 : How To Multiply Square Roots

Simplify:

$-\sqrt{6}(\sqrt{5}-\sqrt{2})$

Possible Answers:

$2\sqrt{3}-\sqrt{30}$

$3\sqrt{2}-\sqrt{30}$

$12-\sqrt{30}$

$2\sqrt{3}+\sqrt{30}$

$-\sqrt{30}-2\sqrt{3}$

Correct answer:

$2\sqrt{3}-\sqrt{30}$

Explanation:

To simplify the problem, just distribute the radical to each term in the parentheses.

$\\-\sqrt{6}(\sqrt{5}-\sqrt{2})\\=-\sqrt{30}+\sqrt{12}\\=-\sqrt{30}+2\sqrt{3}$

Report an Error

Example Question #21 : Basic Squaring / Square Roots

Simplify:

$-2\sqrt{5}(7\sqrt{3}+3\sqrt{10})$

Possible Answers:

$-19\sqrt{10}$

$-14\sqrt{15}-30\sqrt{2}$

$-14\sqrt{5}+30\sqrt{2}$

$-14\sqrt{5}-5\sqrt{2}$

$14\sqrt{5}-6\sqrt{2}$

Correct answer:

$-14\sqrt{15}-30\sqrt{2}$

Explanation:

To simplify the problem, just distribute the radical to each term in the parentheses.

$\\-2\sqrt{5}(7\sqrt{3}+3\sqrt{10})\\=-14\sqrt{15}-6\sqrt{50}$

$\\-14\sqrt{15}-6\sqrt{50}\\=-14\sqrt{15}-6*5\sqrt{2}\\=-14\sqrt{15}-30\sqrt{2}$

Report an Error

Example Question #21 : Basic Squaring / Square Roots

Simplify:

$(\sqrt{2}+\sqrt{7})(\sqrt{27}+\sqrt{12})$

Possible Answers:

$5\sqrt{6}+5\sqrt{21}$

$3\sqrt{6}+2\sqrt{2}+2\sqrt{3}+3\sqrt{7}$

$5\sqrt{6}+2\sqrt{21}+3\sqrt{2}$

$2\sqrt{5}+5\sqrt{2}+3\sqrt{6}$

$3\sqrt{3}+2\sqrt{21}$

Correct answer:

$5\sqrt{6}+5\sqrt{21}$

Explanation:

$(\sqrt{2}+\sqrt{7})(\sqrt{27}+\sqrt{12})$

Let's simplify the right parentheses.

$(\sqrt{27}+\sqrt{12})=(3\sqrt{{3}}+2\sqrt{3})=5\sqrt{3}$

Now we can distribute the radical to each term in the parentheses.

$5\sqrt{3}(\sqrt{2}+\sqrt{7})=5\sqrt{6}+5\sqrt{21}$

Report an Error

Example Question #1 : Basic Squaring / Square Roots

If $\sqrt{x}=3^2$ what is $x$ ?

Possible Answers:

$27$

$9$

$3$

$81$

$729$

Correct answer:

$81$

Explanation:

Square both sides:

x = (3²)²= 9² = 81

Report an Error

Example Question #22 : Basic Squaring / Square Roots

Simplify in radical form:

$\sqrt{507}+\sqrt{12}$

Possible Answers:

$\sqrt{519}$

$26\sqrt{3}$

$15\sqrt{3}$

$11\sqrt{6}$

$12\sqrt{6}$

Correct answer:

$15\sqrt{3}$

Explanation:

To simplify, break down each square root into its component factors:

$\sqrt{507}+\sqrt{12}$

$\sqrt{169\cdot 3}+\sqrt{4\cdot 3}$

$\sqrt{13\cdot13\cdot3}\:+\sqrt{2\cdot 2\cdot 3}$

You can remove pairs of factors and bring them outside the square root sign. At this point, since each term shares $\sqrt3$ , you can add them together to yield the final answer:

$13\sqrt{3}+2\sqrt{3}=15\sqrt{3}$

Report an Error

Example Question #32 : Arithmetic

Simplify: $\frac{2\sqrt{3}}{\sqrt{2}}+\frac{4\sqrt{2}}{\sqrt{3}}$

Possible Answers:

$2\sqrt{6}-4\sqrt{2}$

$4\sqrt{3}+\sqrt{2}$

$2\sqrt{6}$

$\frac{7\sqrt{6}}{3}$

None of the other answers

Correct answer:

$\frac{7\sqrt{6}}{3}$

Explanation:

Take each fraction separately first:

(2√3)/(√2) = [(2√3)/(√2)] * [(√2)/(√2)] = (2 * √3 * √2)/(√2 * √2) = (2 * √6)/2 = √6

Similarly:

(4√2)/(√3) = [(4√2)/(√3)] * [(√3)/(√3)] = (4√6)/3 = (4/3)√6

Now, add them together:

√6 + (4/3)√6 = (3/3)√6 + (4/3)√6 = (7/3)√6

Report an Error

Example Question #11 : Square Roots And Operations

Simplify the following expression: $\sqrt{60}+\sqrt{40}+\sqrt{10}$

Possible Answers:

$2\sqrt{15}+3\sqrt{10}$

$4\sqrt{15}+5\sqrt{5}$

$5\sqrt{25}$

$2\sqrt{15}+2\sqrt{20}$

Correct answer:

$2\sqrt{15}+3\sqrt{10}$

Explanation:

Begin by factoring out each of the radicals:

$\sqrt{60}+\sqrt{40}+\sqrt{10}=\sqrt{4*15}+\sqrt{4*10}+\sqrt{10}$

For the first two radicals, you can factor out a $\sqrt{4}$ or :

$2\sqrt{15}+2\sqrt{10}+\sqrt{10}$

The other root values cannot be simply broken down. Now, combine the factors with $\sqrt{10}$ :

$2\sqrt{15}+2\sqrt{10}+\sqrt{10}=2\sqrt{15}+3\sqrt{10}$

This is your simplest form.

Report an Error

Example Question #4 : Square Roots And Operations

Solve for .

Note, $x\ge0$ :

$15\sqrt{x}-10=4\sqrt{x}+4$

Possible Answers:

$\frac{841}{14}$

$\frac{196}{121}$

$\frac{841}{5}$

$\frac{196}{11}$

Correct answer:

$\frac{196}{121}$

Explanation:

Begin by getting your terms onto the left side of the equation and your numeric values onto the right side of the equation:

$15\sqrt{x}-4\sqrt{x}=4+10$

Next, you can combine your radicals. You do this merely by subtracting their respective coefficients:

$11\sqrt{x}=14$

Now, square both sides:

$(11\sqrt{x})^2=(14)^2$

$(11)^2(\sqrt{x})^2=(14)^2$

121x=196

Solve by dividing both sides by 121 :

$x=\frac{196}{121}$

Report an Error

View SAT Mathematics Tutors

Alexandra
Certified Tutor

Georgia State University, Bachelor of Fine Arts, Studio Art (Photography).

View SAT Mathematics Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

View SAT Mathematics Tutors

Noah
Certified Tutor

Bard College, Bachelors, Philosophy and Creative Writing (Dual Major). Sarah Lawrence College, Master of Fine Arts, Creative ...

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in Miami, SSAT Courses & Classes in Washington DC, ACT Courses & Classes in Houston, ACT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in New York City, SSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Atlanta, GRE Courses & Classes in Atlanta, GMAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Denver

Popular Test Prep

GRE Test Prep in San Diego, ISEE Test Prep in Washington DC, SAT Test Prep in Washington DC, SAT Test Prep in Houston, ACT Test Prep in Dallas Fort Worth, ISEE Test Prep in San Diego, SSAT Test Prep in Atlanta, GRE Test Prep in Atlanta, LSAT Test Prep in Phoenix, ACT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Square Roots and Operations

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #11 : How To Multiply Square Roots

Example Question #12 : How To Multiply Square Roots

Example Question #13 : How To Multiply Square Roots

Example Question #21 : Basic Squaring / Square Roots

Example Question #21 : Basic Squaring / Square Roots

Example Question #1 : Basic Squaring / Square Roots

Example Question #22 : Basic Squaring / Square Roots

Example Question #32 : Arithmetic

Example Question #11 : Square Roots And Operations

Example Question #4 : Square Roots And Operations

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: