Anytime a negative number is added, it is similar to subtraction.  Recovert the expression to the correct form.  Simplify.

The correct answer is .

In order to add the negative numbers, we need to eliminate the double signs and the parentheses.  A positive and a negative sign will result in a negative sign.

Evaluate the terms on the right.

The answer is:  

Let's reductively consider what this data tells us.

Consider each group (a,b,c) as a group of signs.

From abc < 0, we know that the following are possible:

(–, +, +), (+, –, +), (+, +, –), (–, –, –)

From ab > 0, we know that we must eliminate (–, +, +) and (+, –, +)

From bc > 0, we know that we must eliminate (+, +, –)

Therefore, any of our answers must hold for (–, –, –)

This eliminates immediately a > 0, b > 0

Likewise, it eliminates a – b > 0 because we do not know the relative sizes of a and b. This could therefore be positive or negative.

Finally, ac is a product of negatives and is therefore positive. Hence ac < 0 does not hold.

We are left with a + b < 0, which is true, for two negatives added must be negative.

First, it will help us to determine which of the answer choices are positive and which are negative. 

Because n is positive, we know that n² is positive, because any number squared is positive. Similarly, 1/n² is also positive. 

Let's look at the answer choice –1/n. This must be negative, because a negative number divided by a positive one will give us a negative number. Similarly, –1/n³ will also be negative. 

The last choice is n³ – 1. We are told that 0 < n < 1. Because n is a positive value less than one, we know that 0 < n³ < n² < n < 1. In other words, n³ will be a small positive value, but it will still be less than one. Thus, because n³ < 1, if we subtract 1 from both sides, we see that n³ – 1 < 0. Therefore, n³ - 1 is a negative value.

All negative numbers are less than positive numbers. Thus, we can eliminate n² and 1/n², which are both positive. We are left with –1/n, –1/n³, and n³ – 1.

Let us compare –1/n and –1/n³. First, let us assume that –1/n < –1/n³.

–1/n < –1/n³

Multiply both sides by n³. We don't need to switch the signs because n³ is positive.

–n² < –1

Multiply both sides by –1. 

n² > 1.

We know that n² will only be bigger than 1 when n > 1 or if n < –1. But we know that 0 < n < 1, so –1/n is not less than –1/n³. Therefore, –1/n³ must be smaller. 

Finally, let's compare –1/n³ and n³ – 1. Let us assume that –1/n³ < n³ – 1.

–1/n³ < n³ – 1

Multiply both sides by n³.

–1 < n⁶ – n³ 

Add one to both sides.

n⁶ – n³ + 1 > 0. If this inequality is true, then it will be true that –1/n³ is the smallest number.

Here it will be helpful to try some values for n. Let's pick n = 1/2 and see what happens. It will help to use our calculator.

(1/2)⁶ – (1/2)³ + 1 = 0.891 > 0.

Therefore, we suspect that because n⁶ – n³ + 1 > 0, –1/n³ is indeed the smallest number. We can verify this by trying more values of n.

The answer is –1/n³.

The distance between two points is always positive. We calculate lx₂ - x₁l, which will give us the distance between the points.

|14- (-4)| = |14+4| = |18| = 18

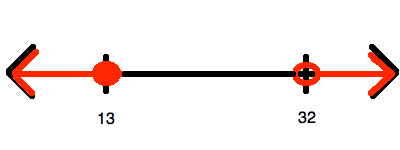
To begin, you must simplify so that you "isolate" , (i.e. at least eliminate any coefficients from it). To do this, divide all of the members of the inequality by :

Now, this inequality represents all of the numbers between 13 and 32.  However, it does include  (hence, getting a closed circle for that value) and does not include  (hence, getting an open circle for that value). Therefore, it looks like:

Since the inequality represents one range of values between two end points (both of which are included, given the sign being "less than or equal"), you know that whatever you answer, it must be convertible to the form:

Now, you know that it is impossible to get this out of the choices that have no absolute values involved in them. Therefore, the only options that make sense are the two having absolute values; however, here you should choose only the ones that have a , for only that will yield a range like this. Thus, we can try both of our options.

The wrong answer is simplified in this manner:

And you can stop right here, for you know you will never have  for the left terminus.

The other option is simplified in this manner:

This is just what you need!

Begin by solving for :

Now, this is represented by drawing an open circle at 6 and graphing upward to infinity:

First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.

Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.

Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).

Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.

The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.