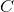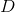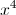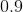Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Decimals

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #361 : Arithmetic

Numberline 1

In the above number line, which point comes closest to $\frac{18}{29}$ ?

Possible Answers:

Correct answer:

Explanation:

Divide numerator 18 by denominator 29 to find the decimal equivalent of the fraction $\frac{18}{29}$ :

Division

The result is slightly higher than 0.62 - the point on the number line.

Report an Error

Example Question #1 : Decimals

Write 0.45 as a fraction.

Possible Answers:

$\frac{5}{9}$

$\frac{2}{5}$

$\frac{3}{4}$

$\frac{11}{20}$

$\frac{9}{20}$

Correct answer:

$\frac{9}{20}$

Explanation:

.45 is equivalent to 45 out of 100, or $\frac{45}{100}$ .

Divide both the numerator and denominator by 5 to simplify the fraction:

$\frac{9}{20}$

Report an Error

Example Question #21 : Decimals

A tub of food contains 0.5 pounds of vegetables, 1.75 pounds of lard, and pounds of sausage. What is its total weight as an improper fraction?

Possible Answers:

$\frac{17}{4}$

$\frac{69}{4}$

$\frac{91}{8}$

$\frac{18}{4}$

$\frac{83}{4}$

Correct answer:

$\frac{69}{4}$

Explanation:

To begin with, it is easiest just to add these decimals together using your calculator:

0.5+1.75+15=17.25

Now, this is the same thing as:

17 + 0.25

We can rewrite this:

$17 + \frac{1}{4}$

To find this, you need to give the two numbers a common denominator:

$17 + \frac{1}{4} = \frac{68}{4}+\frac{1}{4}=\frac{69}{4}$

This is your answer.

Report an Error

Example Question #5 : Decimals

What is the fractional equivalent of 0.33 ?

Possible Answers:

$\frac{33}{100}$

$\frac{333}{1000}$

$\frac{1}{3}$

$\frac{3}{10}$

Correct answer:

$\frac{33}{100}$

Explanation:

In decimal form 0.33 is said 33 hundredths.

This is equal to

$\frac{33}{100}$ .

This fraction cannot be reduced any further therefore it is in its final answer form.

Report an Error

Example Question #1 : How To Find The Fractional Equivalent Of A Decimal

Convert the decimal to fraction form and reduce it to its simplest form.

0.825

Possible Answers:

$\frac{825}{1000}$

$\frac{33}{40}$

$\frac{13}{25}$

$\frac{165}{200}$

$\frac{21}{55}$

Correct answer:

$\frac{33}{40}$

Explanation:

In order to convert 0.825 to a fraction, you would first begin with $\frac{825}{1000}$ , because the decimal literally reads 825 thousandths. You can reduce by a few times or just begin by dividing both numbers by to get $\frac{33}{40}$ .

$\frac{825}{1000}=\frac{165}{200}=\frac{33}{40}$

Report an Error

Example Question #1 : How To Square A Decimal

If all real values of 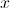$x$ lie between 0 and 1, which of the following is always greater than 1?

Possible Answers:

$x^{2}$

$x+1$

$5x^{2}$

$\frac{x}{10}$

$x^{4}$

Correct answer:

$x+1$

Explanation:

If 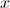$x$ is greater than 0, then adding 1 to $x$ will make it greater than 1. Taking a number between 0 and 1 to a power results in a smaller number.

Report an Error

Example Question #2 : How To Square A Decimal

Evaluate:

0.08²

Possible Answers:

0.00064

0.064

0.0064

0.64

0.00064

Correct answer:

0.0064

Explanation:

0.08 * 0.08

First square 8:

8 * 8 = 64

Then move the decimal four places to the left:

0.0064

Report an Error

Example Question #11 : Decimals

Find the square root of the following decimal:

$\sqrt{.00081}=$

Possible Answers:

0.009

0.09

0.9

0.028

Correct answer:

0.028

Explanation:

The easiest way to find the square root of a fraction is to convert it into scientific notation.

$\dpi{100} \small .00081 = 8.1 \times 10^{-4}$

The key is that the exponent in scientific notation has to be even for a square root because the square root of an exponent is diving it by two. The square root of 9 is 3, so the square root of 8.1 is a little bit less than 3, around 2.8

$\dpi{100} \small \sqrt{8.1 \times 10^{-4}} \approx 2.8 \times 10^{-2} \approx 0.028$

Report an Error

Example Question #2 : How To Find The Square Root Of A Decimal

Find the square root of the following decimal:

$\small \sqrt{0.0049}$

Possible Answers:

$\small 0.07$

$\small 0.7$

$\small 0.007$

$\small 0.022$

Correct answer:

$\small 0.07$

Explanation:

To find the square root of this decimal we convert it into scientific notation.

$\small 0.0049 = 49 \cdot10^{-4}$

Because $\small 10^{-4}$ has an even exponent, we can divide the exponenet by 2 to get its square root.

$\small \sqrt{0.0049} = \sqrt{49}\cdot\sqrt{10^{-4}} = 7\cdot10^{-2} = 0.07$

Report an Error

Example Question #2 : Basic Squaring / Square Roots

Find the square root of the following decimal:

$\small \sqrt{0.025}$

Possible Answers:

$\small 0.005$

$\small 0.625$

$\small 0.158$

$\small 0.05$

Correct answer:

$\small 0.158$

Explanation:

This problem can be solve more easily by rewriting the decimal into scientific notation.

$\small 0.025 = 2.5 \times 10^{-2}$

Because $\small 10^{-2}$ has an even exponent, we can take the square root of it by dividing it by 2. The square root of 4 is 2, and the square root of 1 is 1, so the square root of 2.5 is less than 2 and greater than 1.

$\small \sqrt{0.025} = \sqrt{2.5}\times \sqrt{10^{-2}} = 1.58\times 10^{-1} = 0.158$

Report an Error

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View SAT Mathematics Tutors

Clinton
Certified Tutor

Rensselaer Polytechnic Institute, Current Undergrad, Biology, General. Albany Medical College, PHD, Molecular and Cellular Ph...

View SAT Mathematics Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ISEE Courses & Classes in Phoenix, Spanish Courses & Classes in Washington DC, ISEE Courses & Classes in Los Angeles, ISEE Courses & Classes in Denver, ISEE Courses & Classes in Philadelphia, SSAT Courses & Classes in San Diego, SSAT Courses & Classes in Houston, SAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Seattle, GMAT Courses & Classes in Chicago

Popular Test Prep

ISEE Test Prep in Washington DC, LSAT Test Prep in Denver, GRE Test Prep in Denver, ISEE Test Prep in New York City, LSAT Test Prep in Boston, ISEE Test Prep in Denver, GMAT Test Prep in Chicago, GMAT Test Prep in Phoenix, ACT Test Prep in Dallas Fort Worth, SAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Decimals

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #361 : Arithmetic

Example Question #1 : Decimals

Example Question #21 : Decimals

Example Question #5 : Decimals

Example Question #1 : How To Find The Fractional Equivalent Of A Decimal

Example Question #1 : How To Square A Decimal

Example Question #2 : How To Square A Decimal

Example Question #11 : Decimals

Example Question #2 : How To Find The Square Root Of A Decimal

Example Question #2 : Basic Squaring / Square Roots

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: