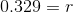All SAT Math Resources
Example Questions
Example Question #191 : Algebraic Functions
The average number of college graduates per year is modeled by the equation 

The number of college graduates each year
The average number of college graduates each year
The estimated decrease in the average number of college graduates each year
The estimated increase in the average number of college graduates each year
The estimated increase in the average number of college graduates each year
The answer is, "The estimated increase in the average number of college graduates each year" because the equation is a model, which is an estimation.
Example Question #191 : Algebraic Functions
Solve for 
Multiply by 
Expand right side
Subtract 
Divide by 
Example Question #192 : Algebraic Functions
If a rocket is shot from the ground, and it takes 

To figure out what the equation is, we need to use the point-slope form.



In this example,
Example Question #192 : Algebraic Functions

Determine the x-intercepts in the graph above.
Not enough information
The x-intercepts are the points on the graph where the 


Example Question #1124 : Algebra
Stuff animals were a strange craze of the 90's. A Cat stuff animal with white paws sold for $6 in 1997. In 2015, the Cat will sell for $1015. What has been the approximate rate of growth for these stuff animal felines?
Use the formula for exponential growth 



Our equation is now:




As a percent, r is about 33%.
Example Question #194 : Algebraic Functions
The population of a city will decrease by 15 percent every 50 years and the population starts at 120,000 people. Construct a function that describes this situation.
To construct a function that describes this situation first identify what is known.
Since this particular situation is talking about population decrease, the function will be an exponential decay.
Recall that an exponential decay function is in the form,
where,
Since the statements says that the population decreases every 50 years we can rewrite the general form to,
Now substituting in the known values, the function can be written.
Example Question #195 : Algebraic Functions

The above graph shows supply and demand for a particular Product. What is the equation for the demand of this product?
We can determine the demand equation by using point slope form.
Point slope form is 



Let 



Now we have
Choose a point 
Example Question #196 : Algebraic Functions

If the equation of the demand line is 

To solve this, all we need to do is set the equations equal to each other.
Now solve for
Example Question #2901 : Sat Mathematics
Amanda has 

This is an exponential growth problem, so let's recall the equation for exponential growth.




First step is to convert 
So in 6 years, Amanda will have 
Example Question #2902 : Sat Mathematics
The equation for the universal gravitation is 








Hint:
The first step is to plug in all the values into the equation.
Now we will solve for 
Take the square root on each side
Certified Tutor
All SAT Math Resources