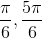We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Sine, Cosine, Tangent

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Trigonometry

Solve for $\theta$ between $[0,2\pi]$ .

$\sin (2\theta )=\frac{1}{2}$

Possible Answers:

$\frac{\pi}{12},\frac{5\pi}{12}$

$\frac{\pi}{3},\frac{2\pi}{3}$

$\frac{\pi}{6},\frac{5\pi}{6}$

$\frac{\pi}{6},\frac{\pi}{3}$

Correct answer:

$\frac{\pi}{12},\frac{5\pi}{12}$

Explanation:

First we must solve for when sin is equal to 1/2. That is at

$\frac{\pi}{6},\frac{5\pi}{6}$

Now, plug it in:

$2\theta =\frac{\pi}{6}\Rightarrow \theta =\frac{\pi}{12}$

$2\theta =\frac{5\pi}{6}\Rightarrow \theta =\frac{5\pi}{12}$

Report an Error

Example Question #9 : Trigonometry

Solve for $\theta$ between $[0,2\pi]$ .

$\cos (2\theta )=\frac{1}{2}$

Possible Answers:

$\frac{\pi}{6},\frac{5\pi}{6}$

$\frac{\pi}{3},\frac{2\pi}{3}$

$\frac{\pi}{3},\frac{5\pi}{3}$

$\frac{\pi}{12},\frac{5\pi}{12}$

Correct answer:

$\frac{\pi}{6},\frac{5\pi}{6}$

Explanation:

First we must solve for when sin is equal to 1/2. That is at

$\frac{\pi}{3},\frac{5\pi}{3}$

Now, plug it in:

$2\theta =\frac{\pi}{3}\Rightarrow \theta =\frac{\pi}{6}\,$

$2\theta =\frac{5\pi}{3}\Rightarrow \theta =\frac{5\pi}{6}$

Report an Error

Example Question #1 : Sine, Cosine, Tangent

In a triangle, ABC , what is the measure of angle A if the side opposite of $\angleA$ angle A is 3 and the adjacent side to angle A is 4?

(Round answer to the nearest tenth of a degree.)

Possible Answers:

$32^{\circ}$

$36.9^{\circ}$

$34.7^{\circ}$

$40^{\circ}$

Correct answer:

$36.9^{\circ}$

Explanation:

To find the measure of angle of A we will use tangent to solve for A. We know that

$tan A=\frac{opposite}{adjacent}$

In our case opposite = 3 and adjacent = 4, we substitute these values in and get:

$tan A= \frac{3}{4}$

Now we take the inverse tangent of each side to find the degree value of A.

$A= tan^{^{-1}}\left(\frac{3}{4}\right)$

A=36.9

Report an Error

Example Question #1 : Trigonometry

If sin(x)=0.5 , what is sin(8x) if is between and $2\pi$ ?

Possible Answers:

-0.5

-1.5

$-\frac{\sqrt{3}}{2}$

$\frac{\sqrt{3}}{2}$

0.5

Correct answer:

$-\frac{\sqrt{3}}{2}$

Explanation:

Recall that $sin(\frac{\pi}{6}) =0.5$ .

Therefore, we are looking for $sin(8*\frac{\pi}{6})$ or $sin(\frac{4\pi}{3})$ .

Now, this has a reference angle of $\frac{\pi}{3}$ , but it is in the third quadrant. This means that the value will be negative. The value of $sin(\frac{\pi}{3})$ is $\frac{\sqrt{3}}{2}$ . However, given the quadrant of our angle, it will be $-\frac{\sqrt{3}}{2}$ .

Report an Error

Example Question #1 : Sine, Cosine, Tangent

Determine the exact value of 8cos(45) .

Possible Answers:

$\frac{\sqrt2}{4}$

$8\sqrt2$

$6\sqrt2$

$4\sqrt2$

$\frac{\sqrt2}{8}$

Correct answer:

$4\sqrt2$

Explanation:

The exact value of cos(45) is the x-value when the angle is 45 degrees on the unit circle.

The x-value of this angle is $\frac{\sqrt2}{2}$ .

$8cos(45)= 8\left(\frac{\sqrt{2}}{2}\right)=4\sqrt2$

Report an Error

Example Question #13 : Trigonometry

Sine

Which of the following is equal to cos(x)?

Possible Answers:

sin(x)

tan(y)

tan(x)

cos(y)

sin(y)

Correct answer:

sin(y)

Explanation:

Remember SOH-CAH-TOA! That means:

$\small cos(x)=\frac{adjacent}{hypotenuse}=\frac{b}{c}$

$\small \small \small sin(x)=\frac{a}{c}$ $\small \small \small \small \small sin(y)=\frac{b}{c}$

$\small \small \small \small cos(y)=\frac{a}{c}$

$\small \small \small \small \small tan(x)=\frac{a}{b}$ $\small \small \small \small tan(y)=\frac{b}{a}$

sin(y) is equal to cos(x)

Report an Error

Example Question #4 : Sin, Cos, Tan

Find the value of $\frac{1}{2}sin(45)+ tan(60)$ .

Possible Answers:

$\sqrt2+\sqrt3$

$\frac{\sqrt2-4\sqrt3}{2}$

$\frac{\sqrt2+4\sqrt3}{2}$

$\frac{\sqrt2+4\sqrt3}{4}$

$\frac{3\sqrt2+\sqrt3}{12}$

Correct answer:

$\frac{\sqrt2+4\sqrt3}{4}$

Explanation:

To find the value of $\frac{1}{2}sin(45)+ tan(60)$ , solve each term separately.

$\frac{1}{2}sin(45)=\frac{1}{2} \cdot \frac{\sqrt2}{2} = \frac{\sqrt2}{4}$

$tan(60) = \sqrt3$

Sum the two terms.

$\frac{\sqrt2}{4}+\sqrt3 = \frac{\sqrt2}{4}+\frac{4\sqrt3}{4} = \frac{\sqrt2+4\sqrt3}{4}$

Report an Error

Example Question #1 : Sine, Cosine, Tangent

Calculate $tan(\frac{4\pi}{3})$ .

Possible Answers:

$\sqrt{3}$

$-\sqrt{3}$

Correct answer:

$\sqrt{3}$

Explanation:

The tangent function has a period of $\pi$ units. That is,

$tan(x+n\pi)=tanx$

for all $n\in\mathbb{Z}$ .

Since $\frac{4\pi}{3}=\frac{\pi}{3}+\pi$ , we can rewrite the original expression $tan(\frac{4\pi}{3})$ as follows:

$tan(\frac{4\pi}{3})=tan(\frac{\pi}{3}+\pi)$

$=tan(\frac{\pi}{3})$

$=\frac{sin(\frac{\pi}{3})}{cos(\frac{\pi}{3})}$

$=\frac{(\frac{\sqrt{3}}{2})}{(\frac{1}{2})}$

$=\sqrt{3}$

Hence,

$tan(\frac{4\pi}{3})=\sqrt{3}$

Report an Error

Example Question #11 : Trigonometry

Calculate $cos(\frac{5\pi}{3})$ .

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

$\frac{\sqrt{3}}{2}$

$-\frac{\sqrt{3}}{2}$

Correct answer:

$\frac{1}{2}$

Explanation:

First, convert the given angle measure from radians to degrees:

$cos(\frac{5\pi}{3})=cos(300^{\circ})$

Next, recall that $300^{\circ}$ lies in the fourth quadrant of the unit circle, wherein the cosine is positive. Furthermore, the reference angle of $300^{\circ}$ is

$360^{\circ}-300^{\circ}=60^{\circ}$

Hence, all that is required is to recognize from these observations that

$cos(\frac{5\pi}{3})=cos(300^{\circ}) =cos(60^{\circ})$ ,

which is $\frac{1}{2}$ .

Therefore,

$cos(\frac{5\pi}{3})=\frac{1}{2}$

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Erik
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Physics. University of California-San Diego, Master of Scien...

View SAT Subject Test in Mathematics Level 1 Tutors

Omar
Certified Tutor

Arizona State University, Bachelors, Civil Engineering.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Boston, Biology Tutors in Houston, Biology Tutors in Chicago, ACT Tutors in San Francisco-Bay Area, Reading Tutors in Seattle, Reading Tutors in Washington DC, Chemistry Tutors in Houston, SAT Tutors in Boston, Reading Tutors in Miami, Spanish Tutors in Boston

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in San Diego, GMAT Courses & Classes in Boston, SSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Phoenix, ISEE Courses & Classes in Phoenix, SAT Courses & Classes in Phoenix, ACT Courses & Classes in Seattle, GMAT Courses & Classes in San Diego, LSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

MCAT Test Prep in Miami, ISEE Test Prep in Seattle, LSAT Test Prep in Philadelphia, LSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Houston, SSAT Test Prep in Philadelphia, SAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Phoenix, SAT Test Prep in Washington DC, MCAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Sine, Cosine, Tangent

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #1 : Trigonometry

Example Question #9 : Trigonometry

Example Question #1 : Sine, Cosine, Tangent

Example Question #1 : Trigonometry

Example Question #1 : Sine, Cosine, Tangent

Example Question #13 : Trigonometry

Which of the following is equal to cos(x)?

sin(y) is equal to cos(x)

Example Question #4 : Sin, Cos, Tan

Example Question #1 : Sine, Cosine, Tangent

Example Question #11 : Trigonometry

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: