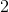We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Data Analysis and Statistics

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 10 11 12 … 15 16 Next →

Example Question #39 : Median

A school district has determined that the most vaulable way to evaluate success is by using the median of all the test scores as the basis. With this in mind, find the median scores of 77, 80, 35, 76, 99, 95, 86, 65, 72, 56, and 21?

Possible Answers:

$\small 72$

$\small 76$

$\small 77$

$\small 65$

$\small 78$

Correct answer:

$\small 76$

Explanation:

The key to solving this problem is to first write the numbers in ascending order.

77, 80, 35, 76, 99, 95, 86, 65, 72, 56, 21

21, 35, 56, 65, 72, 76, 77, 80, 86, 95, 99

After this you will find the middle number of the set which turns out to be $\small 76$ .

21, 35, 56, 65, 72, 76, 77, 80, 86, 95, 99

Report an Error

Example Question #40 : Median

What is the median of the function f(x)= x^2 -1 when (x=-6, -1, 0, 2, 4) ?

Possible Answers:

$\frac{25}{2}$

Correct answer:

Explanation:

We first plug each of the values into the function:

f(-6)=(-6)^2 - 1 = 35

f(-1)=(-1)^2 - 1 = 0

f(0)=(0)^2 - 1 = -1

f(2)=(2)^2 - 1 = 3

f(4)=(4)^2 - 1 = 15

Next, we put the answers in order from least to greatest:

-1, 0, 3, 15, 35

Now, to find the median, we find the value that is in the middle of the data set. Since our data set has an odd number of entries the median will be the value that have an equal number of values to either side of it. In this particular case that value lies at the third entry which is 3.

Report an Error

Example Question #71 : Data Analysis And Statistics

Find the median of: $\{2,4,7,11,17\}$

Possible Answers:

Correct answer:

Explanation:

Step 1: Define median...

The median of a set is the middle number, if the amount of numbers in a given set is odd. The median of a set with an even amount of numbers is the average of the two middle numbers in the set.

Step 2: Find the median of this set..

There is an odd number of numbers...

So, we take the middle number...

The middle number is .

So, is the median.

Report an Error

Example Question #72 : Data Analysis And Statistics

Find the median of the following set:

12, 5, 7, 15,21,17,16,13,12

Possible Answers:

Correct answer:

Explanation:

To find the median, find the number that is in the middle of the set when all of the numbers are ordered from smallest to largest.

12, 5, 7, 15,21,17,16,13,12

First order the numbers from smallest to largest:

5,7,12,12,13,15,16,17,21

In this case, the number in the middle of the set and our answer is:

Report an Error

Example Question #73 : Data Analysis And Statistics

Find the median of the following set:

41,38,27,42,35,38,44

Possible Answers:

Correct answer:

Explanation:

To find the median, find the number that is in the middle of the set when all of the numbers are ordered from smallest to largest.

41,38,27,42,35,38,44

First order the numbers in the set from smallest to largest:

27,35,38,38,41,42,44

In this case, our answer and the middle number of the set is:

Report an Error

Example Question #74 : Data Analysis And Statistics

Find the median of the following set:

6,91,12,31,12

Possible Answers:

Correct answer:

Explanation:

To find the median, find the number that is in the middle of the set when all of the numbers are ordered from smallest to largest.

6,91,12,31,12

First order the numbers in the set from smallest to largest:

6,12,12,31,91

In this case, our answer and the middle number of the set is:

Report an Error

Example Question #75 : Data Analysis And Statistics

Identify the median of the following numbers: [-4,9,3,27,-10]

Possible Answers:

Correct answer:

Explanation:

Arrange the numbers in chronological order from least to greatest.

$[-4,9,3,27,-10]\rightarrow [ -10,-4,3,9,27]$

The median is the central number.

The answer is:

Report an Error

Example Question #72 : Data Analysis And Statistics

Identify the median: [-1,0,-1,0,1,0,-3,3]

Possible Answers:

$-\frac{1}{2}$

$-\frac{1}{4}$

$\frac{1}{2}$

$-\frac{1}{8}$

Correct answer:

Explanation:

Rearrange the data set from least to greatest.

$[-1,0,-1,0,1,0,-3,3]\rightarrow [-3,-1,-1,0,0,0,1,3]$

Since this data set is even, the median the average of the central two numbers.

$\frac{0+0}{2} = 0$

The answer is:

Report an Error

Example Question #741 : Sat Subject Test In Math I

Find the mode of the following set of numbers:

5,3,2,3,3,7,9,2

Possible Answers:

Correct answer:

Explanation:

The mode of a set of numbers is the one that appears most often. Thus, our answer is .

Report an Error

Example Question #742 : Sat Subject Test In Math I

Find the mode of the following set of numbers:

4,1,-2,5,1,8,9

Possible Answers:

Correct answer:

Explanation:

The mode is the number that occurs the most frequently, so our answer is .

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 10 11 12 … 15 16 Next →

View SAT Subject Test in Mathematics Level 1 Tutors

Alena
Certified Tutor

Mogilevsky State Pedagogical Institute, Bachelor in Arts, Mathematics. Mogilevsky State Pedagogical Institute, Masters, Mathe...

View SAT Subject Test in Mathematics Level 1 Tutors

Alexander
Certified Tutor

Cornell University, Bachelor of Science, Biological/Biosystems Engineering. Cleveland State University, Doctor of Philosophy,...

View SAT Subject Test in Mathematics Level 1 Tutors

Fathima
Certified Tutor

BITS Pilani Goa, Doctorate (PhD), Mathematics.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Washington DC, Chemistry Tutors in Miami, GMAT Tutors in New York City, ISEE Tutors in Chicago, Reading Tutors in Phoenix, MCAT Tutors in Philadelphia, English Tutors in San Francisco-Bay Area, Reading Tutors in Seattle, SAT Tutors in San Diego, Biology Tutors in Chicago

Popular Courses & Classes

ISEE Courses & Classes in Boston, GRE Courses & Classes in San Diego, SSAT Courses & Classes in Chicago, Spanish Courses & Classes in Denver, GMAT Courses & Classes in Denver, ISEE Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Washington DC, MCAT Courses & Classes in Los Angeles, ACT Courses & Classes in Los Angeles, Spanish Courses & Classes in New York City

Popular Test Prep

GRE Test Prep in Philadelphia, ACT Test Prep in Atlanta, MCAT Test Prep in Philadelphia, ACT Test Prep in Los Angeles, SSAT Test Prep in San Diego, SAT Test Prep in Philadelphia, GMAT Test Prep in Miami, GMAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Miami, LSAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Data Analysis and Statistics

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #39 : Median

Example Question #40 : Median

Example Question #71 : Data Analysis And Statistics

Example Question #72 : Data Analysis And Statistics

Example Question #73 : Data Analysis And Statistics

Example Question #74 : Data Analysis And Statistics

Example Question #75 : Data Analysis And Statistics

Example Question #72 : Data Analysis And Statistics

Example Question #741 : Sat Subject Test In Math I

Example Question #742 : Sat Subject Test In Math I

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: