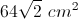All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A Square
A circle with a radius 2 in is inscribed in a square. What is the perimeter of the square?
12 in
28 in
24 in
16 in
32 in
16 in
To inscribe means to draw inside a figure so as to touch in as many places as possible without overlapping. The circle is inside the square such that the diameter of the circle is the same as the side of the square, so the side is actually 4 in. The perimeter of the square = 4s = 4 * 4 = 16 in.
Example Question #2 : How To Find The Perimeter Of A Square
Square X has 3 times the area of Square Y. If the perimeter of Square Y is 24 ft, what is the area of Square X, in sq ft?
72
54
144
108
112
108
Find the area of Square Y, then calculate the area of Square X.
If the perimeter of Square Y is 24, then each side is 24/4, or 6.
A = 6 * 6 = 36 sq ft, for Square Y
If Square X has 3 times the area, then 3 * 36 = 108 sq ft.
Example Question #291 : Plane Geometry
A square has an area of 
The area of the given square is given by 

Example Question #611 : Geometry
If the area of a square is 


Not Enough Information
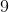

The diagonal of a square creates two special 45-45-90 triangles, meaning that the diagonal of a square is just the length of one side of the square multiplied by the square root of 2.
In this problem, you can figure out the length of one side of the square by finding the square root of the area (which is equal to a side length), then multiplying that number by the square root of 2.
Example Question #1 : Squares
ABCD and EFGH are squares such that the perimeter of ABCD is 3 times that of EFGH. If the area of EFGH is 25, what is the area of ABCD?
25
5
15
75
225
225
Assign variables such that
One side of ABCD = a
and One side of EFGH = e
Note that all sides are the same in a square. Since the perimeter is the sum of all sides, according to the question:
4a = 3 x 4e = 12e or a = 3e
From that area of EFGH is 25,
e x e = 25 so e = 5
Substitute a = 3e so a = 15
We aren’t done. Since we were asked for the area of ABCD, this is a x a = 225.
Example Question #41 : Quadrilaterals
A square has an area of 36. If all sides are doubled in value, what is the new area?
72
144
132
108
48
144
Let S be the original side length. S*S would represent the original area. Doubling the side length would give you 2S*2S, simplifying to 4*(S*S), giving a new area of 4x the original, or 144.
Example Question #2 : How To Find The Area Of A Square
If the perimeter of a square is equal to twice its area, what is the length of one of its sides?
Area of a square in terms of each of its sides:
Area = S x S
Perimeter of a square:
Perimeter = 4S
So if 'the perimeter of a square is equal to twice its area':
2 x Area = Perimeter
2 x [S x S] = [4S]; divide by 2:
S x S = 2S; divide by S:
S = 2
Example Question #1 : How To Find The Area Of A Square
Freddie is building a square pen for his pig. He plans to buy x feet of fencing to build the pen. This will result in a pen with an area of p square feet. Unfortunately, he only has enough money to buy one third of the planned amount of fencing. Which expression represents the area of the pen he can build with this limited amount of fencing?
9p
p/3
3p
p/6
p/9
p/9
If Freddie uses x feet of fencing makes a square, each side must be x/4 feet long. The area of this square is (x/4)2 = x2/16 = p square feet.
If Freddie uses one third of x feet of fencing makes a square, each side must be x/12 feet long. The area of this square is (x/12)2 = x2/144 = 1/9(x2/16) = 1/9(p) = p/9 square feet.
Alternate method:
The scale factor between the small perimeter and the larger perimeter = 1 : 3. Since we're comparing area, a two-dimensional measurement, we can square the scale factor and see that the ratio of the areas is 12 : 32 = 1 : 9.
Example Question #2 : Squares
If the diagonal of a square measures 
This is an isosceles right triangle, so the diagonal must equal 

Example Question #3 : Squares
A square 





The area of 





Certified Tutor
All PSAT Math Resources