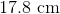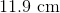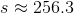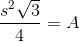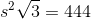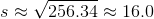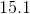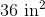All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Surface Area Of A Polyhedron
A regular icosahedron has twenty congruent faces, each of which is an equilateral triangle.
The total surface area of a given regular icosahedron is 400 square centimeters. To the nearest tenth of a centimeter, what is the length of each edge?
The total surface area of the icosahedron is 400 square centimeters; since the icosahedron comprises twenty congruent faces, each has area 
The area of an equilateral triangle is given by the formula
Set 


Example Question #1 : How To Find The Volume Of A Polyhedron

The above depicts a rectangular swimming pool for an apartment. 80% of the pool is six feet deep, and the remaining part of the pool is four feet deep. How many cubic feet of water does the pool hold?
None of the other choices gives the correct answer.
The cross-section of the pool is the area of its surface, which is the product of its length and its width:

Since 80% of the pool is six feet deep, this portion of the pool holds

Since the remainder of the pool - 20% - is four feet deep, this portion of the pool holds

Add them together: the pool holds

Example Question #1 : Tetrahedrons
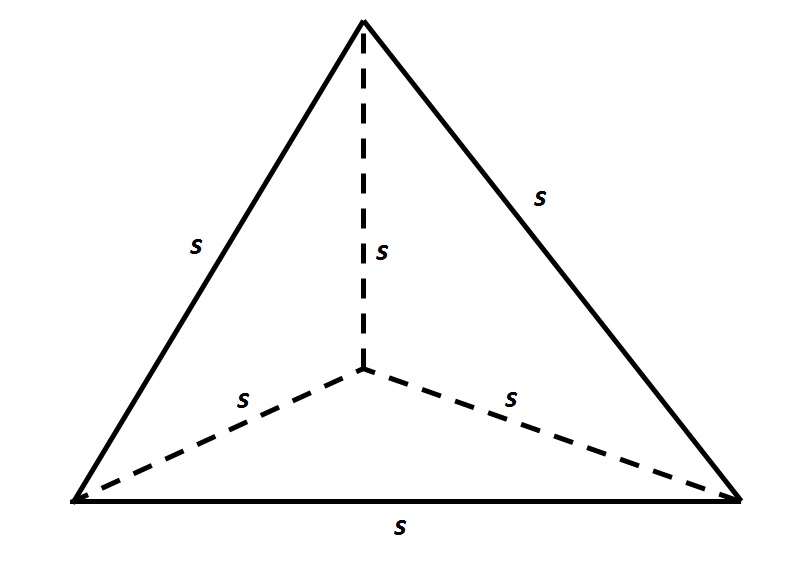
Refer to the above tetrahedron, or four-faced solid. The surface area of the tetrahedron is 444. Evaluate 
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

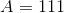
Example Question #71 : Solid Geometry

Note: Figure NOT drawn to scale.
The above triangular pyramid has volume 25. To the nearest tenth, evaluate 
Insufficient information is given to answer the problem.
We are looking for the height of the pyramid.
The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:
The height 
We set 


Example Question #251 : Psat Mathematics

Note: Figure NOT drawn to scale.
Give the volume (nearest tenth) of the above triangular pyramid.
The height of the pyramid is 
The volume of a pyramid can be calculated using the fomula
Example Question #1 : Tetrahedrons
A regular tetrahedron has an edge length of 
The volume of a tetrahedron is found with the equation 

Plug in 4 for the edge length and reduce as much as possible to find the answer:
The volume of the tetrahedron is 
Example Question #1 : How To Find The Surface Area Of A Tetrahedron
A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
The area of an equilateral triangle is given by the formula
Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is
Substitute 

Example Question #2 : How To Find The Surface Area Of A Tetrahedron

Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.
Insufficient information is given to answer the question.
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area
The total surface area is four times this, or about 
Rounded, this is 84.9.
Example Question #1 : Prisms
For a box to fit inside the cupboard, the sum of the height and the perimeter of the box must, at most, be 360 cm. If Jenn has a box that has a height of 40 cm and a length of 23 cm, what is the greatest possible width of the box?
137 cm
297 cm
207 cm
13 cm
0.4 cm
137 cm
First we write out the equation we are given. H + (2L +2W) = 360. H = 40 and L = 23
40 + (2(23) + 2W) = 360
40 + (46 + 2W) = 360
46 + 2W = 320
2W = 274
W = 137
Example Question #1 : How To Find The Length Of An Edge Of A Prism
The volume of a rectangular prism is 80 cm3. The length, width, and height of the prism are each an integer number of cm. If the dimensions form three terms of an arithmetic sequence, find the average of the three dimensions.
8
6
5
7
4
5
Method 1:
Trial and error to find a combination of factors of 80 that differ by the same amount will eventually yield 2, 5, 8. The average is 5.
Method 2:
Three terms of an arithmetic sequence can be written as x, x+d, and x+2d. Multiply these together using the distributive property to find the volume and the following equation results:
x3 + 3dx2 + 2d2x - 80 = 0
Find an integer value of x that creates an integer solution for d. Try x=1 and we see the equation 1 + 3d + 2d2 - 80 = 0 or 2d2 + 3d -79 = 0. The determinant of this quadratic is 641, which is not a perfect square. Therefore, d is not an integer when x=1.
Try x=2 and we see the equation 8 + 12d + 4d2 - 80 = 0 or d2 + 3d - 18 = 0. This is easily factored to (d+6)(d-3)=0 so d=-6 or d=3. Since a negative value of d will result in negative dimensions of the prism, d must equal 3. Therefore, when substituting x=2 and d=3, the dimensions x, x+d, and x+2d become 2, 5, and 8. The average is 5.
Certified Tutor
Certified Tutor
All PSAT Math Resources