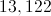First, let us use the definiton of f(x) to find f(10).

f(x) = (2 – x)^(x/3)

f(10) = (2 – 10)^(10/3)

= (–8)^(10/3)

In order to evaluate the above expression, we can make use of the property of exponents that states that a^bc = (a^b)^c = (a^c)^b.

(–8)^(10/3) = (–8)^10(1/3) = ((–8)^(1/3))¹⁰.

(–8)^(1/3) requires us to take the cube root of –8. The cube root of –8 is –2, because (–2)³ = –8.

Let's go back to simplifying ((–8)^(1/3))¹⁰.

((–8)^(1/3))¹⁰ = (–2)¹⁰ = f(10)

We are asked to find n such that 4ⁿ = (–2)¹⁰. Let's rewrite 4ⁿ with a base of –2, because (–2)² = 4.

4ⁿ = ((–2)²)ⁿ = (–2)²ⁿ = (–2)¹⁰

In order to (–2)²ⁿ = (–2)¹⁰, 2n must equal 10.

2n = 10

Divide both sides by 2.

n = 5.

The answer is 5.

In order to solve this equation, we are going to need to use a common base. Because 2, 4, 8, and 16 are all powers of 2, we can rewrite both sides of the equation using 2 as a base. Since 2² = 4, 2³ = 8, and 2⁴ = 16, we can rewrite the original equation as follows:

2ⁿ * 4ⁿ * 8ⁿ * 16 = 2^–n * 4^–n * 8^–n

2ⁿ(2²)ⁿ(2³)ⁿ(2⁴) = 2^–n(2²)^–n(2³)^–n

Now, we will make use of the property of exponents which states that (a^b)^c = a^bc.

2ⁿ(2²ⁿ)(2³ⁿ)(2⁴) = 2^–n(2^–2n)(2^–3n)

Everything is now written as a power of 2. We can next apply the property of exponents which states that a^ba^c = a^b+c.

2^(n+2n+3n+4) = 2^{(–n + –2n + –3n)}

We can now set the exponents equal and solve for n.

n + 2n + 3n + 4 = –n + –2n + –3n

Let's combine the n's on both sides.

6n + 4 = –6n

Add 6n to both sides.

12n + 4 = 0

Subtract 4 from both sides.

12n = –4

Divide both sides by 12.

n = –4/12 = –1/3

The answer is –1/3.

First, we need to solve 125^2x–4 = 625^7–x . When solving equations with exponents, we usually want to get a common base. Notice that 125 and 625 both end in five. This means they are divisible by 5, and they could be both be powers of 5. Let's check by writing the first few powers of 5.

5¹ = 5

5² = 25

5³ = 125

5⁴ = 625

We can now see that 125 and 625 are both powers of 5, so let's replace 125 with 5³ and 625 with 5⁴. 

(5³)^2x–4 = (5⁴)^7–x

Next, we need to apply the rule of exponents which states that (a^b)^c = a^bc .

5^3(2x–4) = 5^4(7–x)

We now have a common base expressed with one exponent on each side. We must set the exponents equal to one another to solve for x.

3(2x – 4) = 4(7 – x)

Distribute the 3 on the left and the 4 on the right.

6x – 12 = 28 – 4x

Add 4x to both sides.

10x – 12 = 28

Add 12 to both sides.

10x = 40

Divide by 10 on both sides.

x = 4

However, the question asks us for the largest prime factor of x. The only factors of 4 are 1, 2, and 4. And of these, the only prime factor is 2. 

The answer is 2. 

When an exponent is raised to a power, we multiply. But when two exponents with the same base are multiplied, we add them. So (x³)² = x^3*2 = x⁶. Then (x³)² * x^–2 = x⁶ * x^–2 = x^6 – 2 = x⁴.

We can break up the equation into two smaller equations involving only x and y. Then, once we solve for x and y, we can find the value of .

 must be negative because it has an odd power and  and  have even powers above. But  and  could be positive or negative, so none of the scenarios has to be true.

Hence the correct answer will be

If

Then

and

Hence

(x³y⁶z)(x²yz³)

The paraentheses are irrelevant. Rearrange to combine like terms.

x³x²y⁶y¹z¹z³

When you multiply variables with exponents, simply add the exponents together.

x³⁺² y⁶⁺¹ z¹⁺³

x⁵y⁷z⁴

To find the answer we can apply the equation of population  where  is the number of hours.