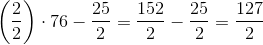We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Complex Fractions

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find A Complex Fraction

Simplify:

$\frac{1- \frac{2}{x}}{1+ \frac{2}{x^{2}}}$

Possible Answers:

$\frac{ x^{2}+2x}{ x^{2}+2}$

$\frac{ x^{2}-2 }{ x^{2}+2}$

$\frac{ x^{2}-2x}{ x^{2}+2}$

$\frac{x}{x+2}$

$\frac{x-2}{x+2}$

Correct answer:

$\frac{ x^{2}-2x}{ x^{2}+2}$

Explanation:

Simplify the numerator and the denominator, then divide, as follows:

$\frac{1- \frac{2}{x}}{1+ \frac{2}{x^{2}}}$

$=\frac{\frac{1 \cdot x}{x} - \frac{2}{x}}{\frac{1 \cdot x^{2}}{x^{2}} + \frac{2}{x^{2}}}$

$=\frac{\frac{ x}{x} - \frac{2}{x}}{\frac{x^{2}}{x^{2}} + \frac{2}{x^{2}}}$

$=\frac{\frac{ x-2}{x} }{\frac{x^{2}+2}{x^{2}} }$

$= \frac{ x-2}{x} \div \frac{x^{2}+2}{x^{2}}$

$= \frac{ x-2}{x} \cdot \frac{x^{2}}{x^{2}+2}$

$= \frac{ x-2}{1} \cdot \frac{x }{x^{2}+2}$

$= \frac{ x^{2}-2x}{ x^{2}+2}$

Report an Error

Example Question #2 : Complex Fractions

Evaluate:

$\frac{3+\frac{1}{4}}{3-\frac{1}{4}}$

Possible Answers:

$\frac{132}{16}$

$\frac{13}{11}$

$\frac{11}{13}$

$\frac{16}{132}$

Correct answer:

$\frac{13}{11}$

Explanation:

Simplify the numerator and the denominator, then divide, as follows:

$\frac{3+\frac{1}{4}}{3-\frac{1}{4}}$

$=\frac{ \frac{12}{4}+\frac{1}{4}}{\frac{12}{4}-\frac{1}{4}}$

$=\frac{ \frac{13}{4}}{\frac{11}{4} }$

$= \frac{13}{4}\div \frac{11}{4}$

$= \frac{13}{4}\cdot \frac{4}{11}$

$= \frac{13}{1}\cdot \frac{1}{11}$

$= \frac{13}{11}$

Report an Error

Example Question #1 : Complex Fractions

Solve:

$76-\frac{75}{6}=$

Possible Answers:

$\frac{127}{2}$

$\frac{7}{6}$

$\frac{1}{6}$

Correct answer:

$\frac{127}{2}$

Explanation:

First reduce the fraction. We can divide both the numerator and the denominator by 3.

$\frac{75\div 3}{6\div 3}=\frac{25}{2}$

Now our expression looks like this:

$76-\frac{25}{2}$

When you add or subtract fractions, you need to have the same denominator. The lowest common deonminator here is 2. So we need to multiply and solve:

$\left ( \frac{2}{2}\right)\cdot76-\frac{25}{2}=\frac{152}{2}-\frac{25}{2}=\frac{127}{2}$

Report an Error

View PSAT Mathematics Tutors

Shakeel
Certified Tutor

View PSAT Mathematics Tutors

Hopelyn
Certified Tutor

Oral Roberts University, Bachelor of Science, Social Work. Universidad de SalamancaUniversidad de Salamanca, Bachelor in Arts...

View PSAT Mathematics Tutors

Ayan
Certified Tutor

Vellore Institute of Technology, Bachelor, Chemical Engineering. University of Calgary, Master's/Graduate, Chemical and Petro...

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Philadelphia, Math Tutors in Boston, MCAT Tutors in Phoenix, Spanish Tutors in San Francisco-Bay Area, Biology Tutors in Denver, Computer Science Tutors in Miami, Biology Tutors in Boston, Reading Tutors in Dallas Fort Worth, Chemistry Tutors in Denver, Spanish Tutors in Boston

Popular Courses & Classes

GRE Courses & Classes in Seattle, ACT Courses & Classes in Washington DC, ISEE Courses & Classes in Seattle, SSAT Courses & Classes in Chicago, LSAT Courses & Classes in Boston, MCAT Courses & Classes in Miami, ACT Courses & Classes in Atlanta, MCAT Courses & Classes in Boston, ACT Courses & Classes in Miami, GRE Courses & Classes in San Diego

Popular Test Prep

ACT Test Prep in Atlanta, GRE Test Prep in Miami, GRE Test Prep in Philadelphia, SAT Test Prep in Miami, SSAT Test Prep in Washington DC, SSAT Test Prep in Miami, ACT Test Prep in Washington DC, LSAT Test Prep in Seattle, SSAT Test Prep in Philadelphia, MCAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Complex Fractions

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : How To Find A Complex Fraction

Example Question #2 : Complex Fractions

Example Question #1 : Complex Fractions

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: