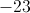All PSAT Math Resources
Example Questions
Example Question #3 : Sequences
Example Question #361 : Arithmetic
In the repeating pattern 9,5,6,2,1,9,5,6,2,1......What is the 457th number in the sequence?
2
5
1
1
9
5
There are 5 numbers in the sequnce.
How many numbers are left over if you divide 5 into 457?
There would be 2 numbers!
The second number in the sequence is 9,5,6,2,1
Example Question #1 : Sequences
If 


Since 
What we notice, however, is that for 


Example Question #151 : Integers
Four consecutive odd integers have a sum of 32. What are the integers?
Consecutive odd integers can be represented as x, x+2, x+4, and x+6.
We know that the sum of these integers is 32. We can add the terms together and set it equal to 32:
x + (x+2) + (x+4) + (x+6) = 32
4x + 12 = 32
4x = 20
x = 5; x+2=7; x+4 = 9; x+6 = 11
Our integers are 5, 7, 9, and 11.
Example Question #361 : Arithmetic
How many integers in the following infinite series are positive: 100, 91, 82, 73 . . . ?
11
13
9
12
10
12
The difference between each number in the series is 9. You can substract nine 11 times from 100 to get 1: 100 – 9x11 = 1. Counting 100, there are 12 positive numbers in the series.
Example Question #1 : How To Find The Common Difference In Sequences
In a sequence of numbers, each term is 
381
378
372
192
384
381
Let's call the first term in the sequence a1 and the nth term an.
We are told that each term is r times larger than the one before it. Thus, we can find the next term in the sequence by multiplying by r.
a1 = a1
a2 = r(a1)
a3 = r(a2) = r(r(a1)) = r2(a1)
a4 = r(a3) = r(r2(a1)) = r3(a1)
an = r(n–1)a1
We can use this information to find r.
The problem gives us the value of the third and the sixth terms.
a3 = r2(a1) = 12
a6 = r5(a1) = 96
Let's solve for a1 in terms of r and a3.
a1 = 12/(r2)
Let's then solve for a1 in terms of r and a6.
a1 = 96/(r5)
Now, we can set both values equal and solve for r.
12/(r2) = 96/(r5)
Multiply both sides by r5 to get rid of the fraction.
12r5/r2 = 96
Apply the property of exponents which states that ab/ac = ab–c.
12r3 = 96
Divide by 12 on both sides.
r3 = 8
Take the cube root of both sides.
r = 2
This means that each term is two times larger than the one before it, or that each term is one half as large as the one after it.
a2 must equal a3 divided by 2, which equals 12/2 = 6.
a1 must equal a2 divided by 2, which equals 6/2 = 3.
Here are the first eight terms of the sequence:
3, 6, 12, 24, 48, 96, 192, 384
The question asks us to find the sum of all the terms less than 250. Only the first seven terms are less than 250. Thus the sum is equal to the following:
sum = 3 + 6 + 12 + 24 + 48 + 96 + 192 = 381
Example Question #11 : Sequences
The first term of an arithmetic sequence is 20; the tenth term is 100. What is the sixteenth term?
Given terms 


Setting 
The 

Setting 
Example Question #11 : Sequences
An arithmetic sequence has as its first term 17. Its tenth term is 
None of the other choices gives the correct response.
None of the other choices gives the correct response.
It is not necessary to determine the common difference or any other terms to answer this question. If we let 
and

The sum of the second and ninth terms is given by the expression
Example Question #12 : Sequences
The first and fourth terms of an arithmetic sequence are, respectively,
and

Which of the following is the common difference of the sequence?
Given terms 



Set 
Example Question #1662 : Sat Mathematics
Which of the following are not natural numbers?
I. 1
II. 0
III. 349010
IV. -2
V. 1/4
II, IV, V
IV, V
II, III, IV, V
I, V
I, IV, V
II, IV, V
Natural numbers are defined as whole numbers 1 and above. II, IV, V are not natural numbers.
Certified Tutor
All PSAT Math Resources