All PSAT Math Resources
Example Questions
Example Question #6 : How To Find The Degree Of A Polynomial
Which of the following monomials has degree 999?
None of the other responses is correct.
The degree of a monomial term is the sum of the exponents of its variables, with the default being 1.
For each monomial, this sum - and the degree - is as follows:






Example Question #1 : How To Find The Degree Of A Polynomial
Find the degree of the polynomial
None of the other answers
The degree of the polynomial is the largest degree of any one of it's individual terms.
The degree of 
The degree of 
The degree of 
The degree of 
The degree of 


Example Question #21 : Algebra
Add the polynomials.
We can add together each of the terms of the polynomial which have the same degree for our variable.
Example Question #21 : Algebra
Step 1: Distribute the negative to the second polynomial:
Step 2: Combine like terms:
Example Question #1 : How To Multiply Polynomials

and

What is 

Example Question #4 : Multiplying And Dividing Polynomials
Multiply:
This product fits the sum of cubes pattern, where 
So
Example Question #1 : Polynomials
If 3 less than 15 is equal to 2x, then 24/x must be greater than
3
4
5
6
3
Set up an equation for the sentence: 15 – 3 = 2x and solve for x. X equals 6. If you plug in 6 for x in the expression 24/x, you get 24/6 = 4. 4 is only choice greater than a.
Example Question #1 : Polynomial Operations
Given a♦b = (a+b)/(a-b) and b♦a = (b+a)/(b-a), which of the following statement(s) is(are) true:
I. a♦b = -(b♦a)
II. (a♦b)(b♦a) = (a♦b)2
III. a♦b + b♦a = 0
I and III
I, II and III
II & III
I only
I and II
I and III
Notice that - (a-b) = b-a, so statement I & III are true after substituting the expression. Substitute the expression for statement II gives ((a+b)/(a-b))((a+b)/(b-a))=((a+b)(b+a))/((-1)(a-b)(a-b))=-1 〖(a+b)〗2/〖(a-b)〗2 =-((a+b)/(a-b))2 = -(a♦b)2 ≠ (a♦b)2
Example Question #2 : Polynomials
If a positive integer a is divided by 7, the remainder is 4. What is the remainder if 3a + 5 is divided by 3?
5
6
3
4
2
2
The best way to solve this problem is to plug in an appropriate value for a. For example, plug-in 11 for a because 11 divided by 7 will give us a remainder of 4.
Then 3a + 5, where a = 11, gives us 38. Then 38 divided by 3 gives a remainder of 2.
The algebra method is as follows:
a divided by 7 gives us some positive integer b, with a remainder of 4.
Thus,
a / 7 = b 4/7
a / 7 = (7b + 4) / 7
a = (7b + 4)
then 3a + 5 = 3 (7b + 4) + 5
(3a+5)/3 = [3(7b + 4) + 5] / 3
= (7b + 4) + 5/3
The first half of this expression (7b + 4) is a positive integer, but the second half of this expression (5/3) gives us a remainder of 2.
Example Question #1 : Polynomial Operations
100
36
45
42
38
42
Certified Tutor
All PSAT Math Resources




















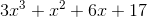


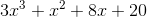
























](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/210807/gif.latex)

](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/210810/gif.latex)







