Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Solve Logarithmic Equations

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1184 : Pre Calculus

Expand this logarithm: $\log_{3}\frac{6x^3y^2}{x^2}$

Possible Answers:

None of the other answers.

$\log_{3}6+\log_{3}x^3+\log_{3}y^2-\log_{3}x^2$

$\log_{3}6+3\log_{3}x+2\log_{3}y+2\log_{3}x$

$\log_{3}6+\log_{3}x^3+\log_{3}y^2+\log_{3}x^2$

$\log_{3}6+3\log_{3}x+2\log_{3}y-2\log_{3}x$

Correct answer:

$\log_{3}6+3\log_{3}x+2\log_{3}y-2\log_{3}x$

Explanation:

$\log_{3}\frac{6x^3y^2}{x^2}$

Use the Quotient property of Logarithms to express on a single line:

$\log_{3}6x^3y^2-x^2$

Use the Product property of Logarithms to expand the two terms further:

$\log_{3}6+\log_{3}x^3+\log_{3}y^3-\log_{3}x^2$

Finally use the Power property of Logarithms to remove all exponents:

$\log_{3}6+3\log_{3}x+2\log_{3}y-2\log_{3}x$

The expression is now fully expanded.

Report an Error

Example Question #32 : Solve Logarithmic Equations

Expand the following logarithm:

$\log(\frac{5x^4}{7})$

Possible Answers:

$\frac{\log(5)\cdot 4\log(x)}{-\log(7)}$

$4\log(5)+4\log(x)-4\log(7)$

$\log(5)+4\log(x)-\log(7)$

$\frac{\log(5)\cdot4\log(x)}{\log(7)}$

Correct answer:

$\log(5)+4\log(x)-\log(7)$

Explanation:

Expand the following logarithm:

$\log(\frac{5x^4}{7})$

To expand this log, we need to keep in mind 3 rules:

1) When dividing within a $\log$ , we need to subtract

2) When multiplying within a $\log$ , we need to add

3) When raising to a power within a $\log$ , we need to multiply by that number

These will make more sense once we start applying them.

First, let's use rule number 1

$\log(\frac{5x^4}{7})=\log(5x^4)-\log(7)$

Next, rule 2 sounds good.

$\log(5x^4)-\log(7)=\log(5)+\log(x^4)-\log(7)$

Finally, use rule 3 to finish up!

$\log(5)+\log(x^4)-\log(7)=\log(5)+4\log(x)-\log(7)$

Making our answer

$\log(5)+4\log(x)-\log(7)$

Report an Error

Example Question #33 : Solve Logarithmic Equations

Completely expand this logarithm: $\ln\frac{x^4\sqrt{y}}{n^5}$

Possible Answers:

$4\ln x+\ln y-5\ln n$

$4\ln x-\frac{1}{2}\ln y+5\ln n$

$4\ln x+\frac{1}{2}\ln y+5\ln n$

$4\ln x+\frac{1}{2}\ln y-5\ln n$

$4\ln x+\ln y+5\ln n$

Correct answer:

$4\ln x+\frac{1}{2}\ln y-5\ln n$

Explanation:

$\ln\frac{x^4\sqrt{y}}{n^5}$

Quotient property:

$\ln x^4\sqrt{y}-\ln n^5$

Product property:

$\ln x^4+\ln\sqrt{y}-\ln n^5$

Power property:

$\mathbf{4\ln x+\frac{1}{2} \ln y-5 \ln n}$

Report an Error

Example Question #31 : Solve Logarithmic Equations

Fully expand: $\log(\frac{a^2b}{c})$

Possible Answers:

$\log(2)+\log(a)+\log(b)-\log(c)$

$\log(a^2)+ \log(b)-\log(c)$

$\log(2a^2b)-\log(c)$

$2\log(a)+\log(b)-\log(c)$

$\log(2ab)-\log(c)$

Correct answer:

$2\log(a)+\log(b)-\log(c)$

Explanation:

In order to expand the expression, use the log rules of multiplication and division. Anytime a variable is multiplied, the log is added. If the variable is being divided, subtract instead.

$\log(\frac{a^2b}{c}) = \log(a^2)+ \log(b)-\log(c)$

When there is a power to a variable when it is inside the log, it can be pulled down in front of the log as a coefficient.

$\log(a^2)+ \log(b)-\log(c) = 2\log(a)+\log(b)-\log(c)$

The answer is: $2\log(a)+\log(b)-\log(c)$

Report an Error

Example Question #61 : Properties Of Logarithms

Expand the following:

$\log(2x)+\log(x-1)$

Possible Answers:

$\log\frac{2x}{x-1}$

$\log(2x)+\log(x-1)$

$\log(2x^2-2x)$

$\log(2)+x$

Correct answer:

$\log(2x^2-2x)$

Explanation:

To solve, simply remember that when you add logs, you multiply their insides.

Thus,

$\\\log(2x)+\log(x-1)\\ \\=\log((2x)(x-1))\\ \\=\log(2x^2-2x)$

Report an Error

Example Question #62 : Properties Of Logarithms

Express the following in expanded form.

$\log{\frac{xz}{y}}$

Possible Answers:

$\log{x}+\log{z}-\log{y}$

$\log{x}-\log{z}+\log{y}$

$\log{x}+\log{z}+\log{y}$

$\log{x}-\log{z}-\log{y}$

Correct answer:

$\log{x}+\log{z}-\log{y}$

Explanation:

To solve, simply remember that when adding logs, you multiply their insides and when subtract logs, you divide your insides. You must use this in reverse to solve. Thus,

$\log{\frac{xz}{y}}=\log{xz}-\log{y}=\log{x}+\log{z}-\log{y}$

Report an Error

Example Question #37 : Solve Logarithmic Equations

Completely expand this logarithm:

$\ln \frac{\sqrt{6x-2}}{8}$

Possible Answers:

The answer is not present.

$\ln(6x-2)^{\frac{1}{2}}-\ln 8$

$\frac{1}{2}\ln(6x-2)-\ln 8$

$\frac{1}{2}\ln(6x) -\ln (2)-\ln 8$

$\ln(6x-2)^{\frac{1}{2}}-2.08$

Correct answer:

$\frac{1}{2}\ln(6x-2)-\ln 8$

Explanation:

We expand logarithms using the same rules that we use to condense them.

Here we will use the quotient property

$\ln\frac{u}{v}= \ln u-\ln v$

and the power property

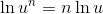
$\ln u^{n}=n\ln u$ .

$\ln \frac{\sqrt{6x-2}}{8}$

Use the quotient property:

$\ln \sqrt{6x-2}-\ln 8$

Rewrite the radical:

$\ln (6x-2)^{\frac{1}{2}}-\ln 8$

Now use the power property:

$\frac{1}{2}\ln (6x-2)-\ln 8$

Report an Error

Example Question #63 : Properties Of Logarithms

Expand the logarithm

$log\,(x^2y^3)$

Possible Answers:

$2log\,x+3log\,y$

$6log\,xy$

$log\,2x+log\,3y$

$log\,x^2-log\,y^3$

Correct answer:

$2log\,x+3log\,y$

Explanation:

In order to expand the logarithmic expression, we use the following properties

$alog\,x=log\,x^a$
$log\,a+log\,b=log\,ab$

As such

$log\,(x^2y^3)=log\,x^2+log\,y^3=2log\,x+3log\,y$

Report an Error

Example Question #64 : Properties Of Logarithms

Given the equation $ln(e^{3x})=15$ , what is the value of ? Use the inverse property to aid in solving.

Possible Answers:

x=3

x=ln3

x=3e

$x=e^{15}$

x=5

Correct answer:

x=5

Explanation:

The natural logarithm and natural exponent are inverses of each other. Taking the of will simply result in the argument of the exponent.

That is $ln(e^{3x})=3x$

Now, 3x=15 , so x=5.

Report an Error

View Pre-Calculus Tutors

Tajrin
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Computer Science.

View Pre-Calculus Tutors

Tracy
Certified Tutor

Clarion University of Pennsylvania, Bachelor of Science, Physics.

View Pre-Calculus Tutors

Yaakoub
Certified Tutor

CUNY Queens College, Bachelor of Science, Finance. Vaughn College of Aeronautics and Technology, Bachelor of Science, Electri...

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Phoenix, Statistics Tutors in New York City, Physics Tutors in Phoenix, ACT Tutors in New York City, Computer Science Tutors in Philadelphia, ACT Tutors in Chicago, SSAT Tutors in Denver, Calculus Tutors in Boston, SSAT Tutors in Dallas Fort Worth, Math Tutors in Seattle

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Chicago, MCAT Courses & Classes in Boston, LSAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Miami, GRE Courses & Classes in San Diego, LSAT Courses & Classes in Houston, MCAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Washington DC, GRE Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in New York City, MCAT Test Prep in Denver, GMAT Test Prep in Denver, SAT Test Prep in Los Angeles, LSAT Test Prep in Miami, LSAT Test Prep in Washington DC, GRE Test Prep in Phoenix, SAT Test Prep in Chicago, ISEE Test Prep in Washington DC, SSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Solve Logarithmic Equations

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1184 : Pre Calculus

Example Question #32 : Solve Logarithmic Equations

Example Question #33 : Solve Logarithmic Equations

Example Question #31 : Solve Logarithmic Equations

Example Question #61 : Properties Of Logarithms

Example Question #62 : Properties Of Logarithms

Example Question #37 : Solve Logarithmic Equations

Example Question #63 : Properties Of Logarithms

Example Question #64 : Properties Of Logarithms

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: