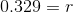Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Pre-Calculus

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #12 : Application Problems

There were 240mg of caffeine in the discontinued energy drink. The decay rate for caffeine in the human bloodstream is around 0.14. If Jackie drinks this energy drink around 8PM, how much caffeine will still be in her system at midnight?

Possible Answers:

420.2 mg

137.1 mg

157.7mg

29.2 mg

119.2mg

Correct answer:

137.1 mg

Explanation:

Because this is a process taking place in the human body, we should use the exponential decay formula involving e:

$A=P*e^{rt}$

where A is the current amount, P is the initial amount, r is the rate of growth/decay, and t is time.

In this case, since the amount of caffeine is decreasing rather than increasing, use r=-0.14 . Between 8PM and midnight, 4 hours pass, so use t=4 . The initial amount of caffeine is given as 240 mg, so use P=240 .

Now evaluate:

$\\ A = 240\cdot e^{-0.14\cdot 4} \\ \\= 240\cdot e^{-0.56} \approx 240 \cdot 0.57 \\ \\= 137.1$

Report an Error

Example Question #1401 : Pre Calculus

Stuff animals were a strange craze of the 90's. A Cat stuff animal with white paws sold for $6 in 1997. In 2015, the Cat will sell for $1015. What has been the approximate rate of growth for these stuff animal felines?

Possible Answers:

$3.2 \%$

$33 \%$

$16.8 \%$

$168 \%$

$13.29 \%$

Correct answer:

$33 \%$

Explanation:

Use the formula for exponential growth y = A*(1+r)^t where y is the current value, A is the initial value, r is the rate of growth, and t is time. Between 1997 and 2015, 18 years passed, so use t=18 . The stuffed animal was originally worth $6, so A=6 . It is now worth $1,015, so y=1015 .

Our equation is now:

$1015 = 6*(1+r)^{18}$ divide by 6:

$169.1\overline{6}=(1+r)^{18}$ take both sides to the power of $\frac{1}{18}=0.0\overline{5}$ :

$1.329 \approx 1+r$ subtract 1

0.329 = r

As a percent, r is about 33%.

Report an Error

Example Question #1 : Use Trigonometric Functions To Calculate The Area Of A Triangle

In triangle ABC , $m\angle C = 30^\circ$ , BC = 40 , and AC = 20 . Find the area of the triangle.

Possible Answers:

800

100

1600

200

400

Correct answer:

200

Explanation:

When given the lengths of two sides and the measure of the angle included by the two sides, the area formula is:

$A = \frac {1}{2}ab\sin C \\$

Plugging in the given values we are able to calculate the area.

$A = \frac {1}{2}\cdot 40\cdot 20 \cdot \sin 30^\circ= 200$

Report an Error

Example Question #2 : Area Of A Triangle

Find the area of this triangle:

Tri area f

Possible Answers:

68 un^ 2

11.81 un^ 2

136 un^ 2

66.97 un^ 2

Correct answer:

68 un^ 2

Explanation:

To find the area, use the formula associated with side, angle, side triangles which states,

$area = \frac{ 1}{2} a b \sin C$

where and are side lengths and is the included angle.

In our case,

$a=8, b=17, C=90^\circ$ .

Plug the values into the area formula and solve.

$area = \frac{ 1}{2} (8 )( 17 ) \cdot \sin( 90 ^ o ) = 68$

Report an Error

Example Question #1 : Area Of A Triangle

Find the area of this triangle:

Tri area d

Possible Answers:

88.11 un^ 2

53.96 un^ 2

82. 99 un ^ 2

212.13 un^ 2

Correct answer:

82. 99 un ^ 2

Explanation:

Use the area formula to find area that is associated with the side angle side theorem for triangles.

$area= \frac{ 1}{2 } a b \sin C$

where and are side lengths and is the included angle.

Plugging these values into the formula above, we arrive at our final answer.

$area = \frac{ 1}{2} (11) (23 ) \sin (41^o ) \approx 82.99$

Report an Error

Example Question #1 : Area Of A Triangle

Find the area of this triangle:

Tri area b

Possible Answers:

25.38 un^ 2

28 un^ 2

23.67 un^ 2

11.83 un^ 2

Correct answer:

11.83 un^ 2

Explanation:

To solve, use the formula for area that is associated with the side angle side theorem for triangles,

$area = \frac{ 1}{2} ab \sin C$

where and are side lengths and is the included angle.

Here we are using 25^o and not 90^o since that is the angle between and .

Therefore,

$a=8,b=7,C=25^\circ$ .

Plugging the above values into the area formula we arrive at our final answer.

$area = \frac{ 1}{2} (8)(7) \sin (25^o ) \approx 11.83$

Report an Error

Example Question #1 : Area Of A Triangle

Find the area of this triangle:

Tri area a

Possible Answers:

48.74 un^ 2

133.91 un^2

48.84 un^2

66.95 un^ 2

Correct answer:

48.74 un^ 2

Explanation:

Find the area using the formula associated the side angle side theorem of a triangle,

$area = \frac{ 1}{2} ab \sin C$

where and are side lengths and is the included angle.

In this particular case,

$a=15, b=19, C=20^\circ$

therefore the area is found to be,

$area = \frac {1}{2} (15)(19) \sin (20^o ) \approx 48.74$ .

Report an Error

Example Question #2 : Use Trigonometric Functions To Calculate The Area Of A Triangle

Find the exact area of a triangle with side lengths of , , and .

Possible Answers:

$\frac{\sqrt {135}}{4}$

1.5

$\frac{\sqrt{17}}{2}$

$\frac{\sqrt{135}}{8}$

2.5

Correct answer:

$\frac{\sqrt {135}}{4}$

Explanation:

Use the Heron's Formula:

$s=\frac{a+b+c}{2}$

$A=\sqrt{s(s-a)(s-b)(s-c)}$

Solve for .

$s=\frac{a+b+c}{2}=\frac{2+3+4}{2}=\frac{9}{2}$

Solve for the area.

$A=\sqrt{s(s-a)(s-b)(s-c)}$

$A=\sqrt{\frac{9}{2}\left(\frac{9}{2}-2\right)\left(\frac{9}{2}-3\right)\left(\frac{9}{2}-4\right)}$

$A=\sqrt{\frac{9}{2}\left(\frac{5}{2}\right)\left(\frac{3}{2}\right)\left(\frac{1}{2}\right)}=\sqrt{\frac{135}{16}}=\frac{\sqrt{135}}{4}$

Report an Error

Example Question #3 : Use Trigonometric Functions To Calculate The Area Of A Triangle

What is the area of a triangle with side lengths , , and ?

Possible Answers:

area=16

area=4

$area=\sqrt{92}$

$area=4\sqrt{6}$

$area=16\sqrt{6}$

Correct answer:

$area=4\sqrt{6}$

Explanation:

We can solve this question using Heron's Formula. Heron's Formula states that:

The semiperimeter is

$s=\frac{1}{2}(a+b+c)$

where , , are the sides of a triangle.

Then the area is

$area=\sqrt{s(s-a)(s-b)(s-c)}$

So if we plug in

$s=\frac{1}{2}(4+5+7)$

$s=\frac{1}{2}(16)$

s=8

So the area is

$area=\sqrt{8(8-4)(8-5)(8-7)}$

$area=\sqrt{96}$

$area=4\sqrt{6}$

Report an Error

Example Question #4 : Use Trigonometric Functions To Calculate The Area Of A Triangle

What is the area of a triangle with sides , , and ?

Possible Answers:

$area=10\sqrt{2}$

area=200

area=10

$area=20\sqrt{2}$

$area=100\sqrt{2}$

Correct answer:

$area=10\sqrt{2}$

Explanation:

We can solve this question using Heron's Formula. Heron's Formula states that:

The semiperimeter is

$s=\frac{1}{2}(a+b+c)$

where , , are the sides of a triangle.

Then the area is

$area=\sqrt{s(s-a)(s-b)(s-c)}$

So if we plug in

$s=\frac{1}{2}(6+5+9)$

$s=\frac{1}{2}(20)$

s=10

So the area is

$area=\sqrt{10(10-6)(10-5)(10-9)}$

$area=\sqrt{200}$

$area=10\sqrt{2}$

Report an Error

View Pre-Calculus Tutors

Chahat
Certified Tutor

Houston Community College, Associate in Science, Mechanical Engineering. Texas A & M University-College Station, Bachelor of ...

View Pre-Calculus Tutors

Chad
Certified Tutor

Gannon University, Bachelor of Science, Chemistry.

View Pre-Calculus Tutors

Ryanto
Certified Tutor

Excelsior College, Albany NY, Bachelor, Business with Math Minor. University of Houston, Master's/Graduate, Accounting.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in New York City, Math Tutors in Phoenix, Chemistry Tutors in Philadelphia, Chemistry Tutors in Houston, Algebra Tutors in New York City, Chemistry Tutors in Phoenix, LSAT Tutors in Seattle, SSAT Tutors in Denver, Chemistry Tutors in Seattle, Spanish Tutors in Phoenix

Popular Courses & Classes

SAT Courses & Classes in Miami, ACT Courses & Classes in Washington DC, LSAT Courses & Classes in Houston, SSAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in New York City, LSAT Courses & Classes in Seattle, Spanish Courses & Classes in Seattle, SSAT Courses & Classes in Boston, MCAT Courses & Classes in Chicago, SAT Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in New York City, GRE Test Prep in New York City, ACT Test Prep in Washington DC, ACT Test Prep in Atlanta, MCAT Test Prep in Atlanta, SAT Test Prep in Chicago, ISEE Test Prep in Los Angeles, MCAT Test Prep in Washington DC, MCAT Test Prep in Philadelphia, LSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Pre-Calculus

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #12 : Application Problems

Example Question #1401 : Pre Calculus

Example Question #1 : Use Trigonometric Functions To Calculate The Area Of A Triangle

Example Question #2 : Area Of A Triangle

Example Question #1 : Area Of A Triangle

Example Question #1 : Area Of A Triangle

Example Question #1 : Area Of A Triangle

Example Question #2 : Use Trigonometric Functions To Calculate The Area Of A Triangle

Example Question #3 : Use Trigonometric Functions To Calculate The Area Of A Triangle

Example Question #4 : Use Trigonometric Functions To Calculate The Area Of A Triangle

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: