First, find the slope of this tangent line by taking the derivative:

Plugging in 1 for x:

So the slope is 4

Now we need to find the y-coordinate when x is 1, so plug 1 in to the original equation:

To write the equation, use point-slope form and then use algebra to change to slope-intercept like the answer choices:

distribute the 4

add 2 to both sides

First, find the slope of the tangent line by taking the first derivative:

To finish determining the slope, plug in the x-value, 2:

the slope is 6

Now find the y-coordinate where x is 2 by plugging in 2 to the original equation:

To write the equation, start in point-slope form and then use algebra to get it into slope-intercept like the answer choices.

distribute the 6

add 8 to both sides

First, take the first derivative in order to find the slope:

To continue finding the slope, plug in the x-value, -2:

Then find the y-coordinate by plugging -2 into the original equation:

The y-coordinate is

Now write the equation in point-slope form then algebraically manipulate it to match one of the slope-intercept forms of the answer choices.

distribute the -5

add to both sides

First distribute the . That will make it easier to take the derivative:

Now take the derivative of the equation:

To find the slope, plug in the x-value -3:

To find the y-coordinate of the point, plug in the x-value into the original equation:

Now write the equation in point-slope, then use algebra to get it into slope-intercept like the answer choices:

 distribute

subtract from both sides

write as a mixed number

 will approach when approaches , so  will be of type  as shown below:

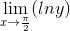
So, we can apply the L’ Hospital's Rule:

since:

hence:

When x=3/2 our denominator is zero so we can't just plug in 3/2 to get our limit. If we look at the numerator when x=3/2 we find that it is zero as well so our numerator can be factored. We see that our limit can be re-written as:

we then can cancel the 2x-3 from the numerator and denominator leaving us with:

and we can just plug in 3/2 into this limit to get 

note: our function is not continuous at x=3/2 but the limit does exist.

To solve this problem we need to expand the term in the numerator 

when we do that we get 

the second degree x terms cancel and we get

now we can cancel our h's in the numerator and denominator to get

then we can just plug 0 in for h and we get our answer

The function has a removable discontinuity at  .  Once a factor of  is "divided out" the resultant function is , which evaluates to  as  approaches 0.

This is a graph of . We know that  is undefined; therefore, there is no value for . But as we take a look at the graph, we can see that as  approaches 0 from the left,  approaches negative infinity. 

This can be illustrated by thinking of small negative numbers.

NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful. 

 is actually infinity, not negative infinity. 

This can be rewritten as follows:

We can substitute , noting that as , : 

, which is the correct choice.