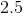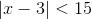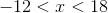Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Special Functions

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Special Functions

Let

$y=\left\{\begin{matrix} 2x&x\leq 0\\ x+9& x>0 \end{matrix}\right.$

What does equal when x=3 ?

Possible Answers:

Correct answer:

Explanation:

Because 3>0 we plug the x value into the bottom equation.

x=3

y=x+9

y=3+9=12

Report an Error

Example Question #2 : Special Functions

Let

$y=\left\{\begin{matrix} x-9&x\leq 0\\ x+9& x>0 \end{matrix}\right.$

What does equal when x=0 ?

Possible Answers:

Correct answer:

Explanation:

Because $0\leq0$ we use the first equation.

y=x-9

Therefore, plugging in x=0 into the above equation we get the following,

y=0-9=-9 .

Report an Error

Example Question #3 : Special Functions

Determine the value of f(1) if the function is

$f(x)=\left\{\begin{matrix} x& x<3\\ \pi&x=3 \\ 4&x>3 \end{matrix}\right.$

Possible Answers:

$f(1)=\pi$

f(1)=1

f(1)=3

f(1)=4

Correct answer:

f(1)=1

Explanation:

In order to determine the value of f(1) of the function we set x=1.

The value comes from the function in the first row of the piecewise function, and as such

f(1)=1

Report an Error

Example Question #4 : Piecewise Functions

Determine the value of f(1) if the function is

$f(x)=\left\{\begin{matrix} \sqrt{x}& 0\leq x<4\\ \3&x=4 \\ e^{-x}&x>4 \end{matrix}\right.$

Possible Answers:

f(1)=1

f(1)=3

$f(1)=\frac{1}{e}$

f(1)=3

Correct answer:

f(1)=1

Explanation:

In order to determine the value of f(1) of the function we set x=1.

The value comes from the function in the first row of the piecewise function, and as such

$f(1)=\sqrt{1}=1$

Report an Error

Example Question #1 : Piecewise Functions

For the function f(x) defined below, what is the value of f(x) when x=3 ?

$f(x)=\left\{\begin{matrix} -x+1&\text{ for }x<1\\ x^{2}-2&\text{ for }1< x< 3\\ 2^{x}&\text{ for }x\geq 3 \end{matrix}$

Possible Answers:

-2

Correct answer:

Explanation:

Evaluate the function for x=3 . Based on the domains of the three given expressions, you would use $2^{x}$ , since is greater than or equal to .

$2^{x}=2^{3}=8$

Report an Error

Example Question #1 : Greatest Integer Functions

If is the greatest integer function, what is the value of F(2.4) ?

Possible Answers:

2.5

Correct answer:

Explanation:

The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was 2.4 , we are looking for an integer less than this, which must be since any smaller integer would by definition not be "greatest".

Report an Error

Example Question #1 : Absolute Value Functions

Which of the following is a point on the following function?

$y=\left | x^2-5x-56\right |+27$

Possible Answers:

(0,0)

(5,-43)

(14,36)

(-27,-27)

(5,83)

Correct answer:

(5,83)

Explanation:

One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.

Our y value will never be negative, so eliminate any options with a negative y-value.

Try (0,0) really quick, since it's really easy

$y=\left | x^2-5x-56\right |+27 \rightarrow 0=\left|0^2-5(0)-56\right|+27=83 \rightarrow 0\neq 83$

The only point that makes sense is (5,83), therefore it is the correct answer

$y=\left | x^2-5x-56\right |+27 \rightarrow 83=\left|5^2-5(5)-56\right|+27=83 \rightarrow 83=83$

Report an Error

Example Question #2 : Absolute Value Functions

Evaluate: $\left | x-3\right |<15$

Possible Answers:

$-12\leq x\leq18$

-12,18

-12<x<18

$x\leq18$

x<18

Correct answer:

-12<x<18

Explanation:

Cancel the absolute value sign by separating the function $\left | x-3\right |<15$ into its positive and negative counterparts.

x-3<15

-(x-3)<15

Evaluate the first scenario.

x-3<15

x<18

Evaluate the second scenario.

-(x-3)<15

x-3>-15

x>-12

The correct answer is:

-12<x<18

Report an Error

Example Question #1 : Absolute Value Functions

If $y=\left |x^3-5x^2+5 \right |$ , then what is the value of when x=3 ?

Possible Answers:

-13

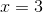
-7

Correct answer:

Explanation:

We evaluate for x=3

y=|(3)^3-5(3)^2+5|

y=|27-45+5|

y=|-13|

Since the absolute value of any number represents its magnitude from and is therefore always positive, the final answer would be y=13

Report an Error

View Pre-Calculus Tutors

Sharon
Certified Tutor

Tabor College, Bachelor of Science, Mathematics Teacher Education. Tabor College, Masters in Education, Education.

View Pre-Calculus Tutors

Rhys
Certified Tutor

Portland State University, Bachelor of Science, Microbiology. Arizona State University, Doctor of Philosophy, Microbiology.

View Pre-Calculus Tutors

Joseph
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mathematics.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Phoenix, Math Tutors in Washington DC, ACT Tutors in Atlanta, MCAT Tutors in Seattle, GRE Tutors in Atlanta, Algebra Tutors in New York City, SAT Tutors in Houston, Spanish Tutors in Chicago, MCAT Tutors in Atlanta, English Tutors in Phoenix

Popular Courses & Classes

LSAT Courses & Classes in New York City, MCAT Courses & Classes in Phoenix, GMAT Courses & Classes in Los Angeles, SAT Courses & Classes in Miami, ACT Courses & Classes in Seattle, ISEE Courses & Classes in Atlanta, Spanish Courses & Classes in Miami, GMAT Courses & Classes in Atlanta, SAT Courses & Classes in Phoenix, MCAT Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in Denver, ACT Test Prep in San Francisco-Bay Area, ACT Test Prep in Phoenix, ACT Test Prep in Seattle, SAT Test Prep in Chicago, GMAT Test Prep in Boston, GRE Test Prep in Denver, ISEE Test Prep in Phoenix, SAT Test Prep in Seattle, ISEE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Special Functions

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1 : Special Functions

Example Question #2 : Special Functions

Example Question #3 : Special Functions

Example Question #4 : Piecewise Functions

Example Question #1 : Piecewise Functions

Example Question #1 : Greatest Integer Functions

Example Question #1 : Absolute Value Functions

Example Question #2 : Absolute Value Functions

Example Question #1 : Absolute Value Functions

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: