When you think of a trigonometric function of the form y=Asin(Bx+C)+D, the amplitude is represented by A, or the coefficient in front of the sine function. While this number is -24, we always represent amplitude as a positive number, by taking the absolute value of it. Therefore, the amplitude of this function is 24. 

The following matches the correct period with its corresponding trig function:

In other words, sin x, cos x, sec x, and csc x all repeat themselves every  units. However, tan x and cot x repeat themselves more frequently, every  units. 

The graph has 3 waves between 0 and , meaning that the length of each of the waves is  divided by 3, or .

In order to write this equation, it is helpful to sketch a graph:

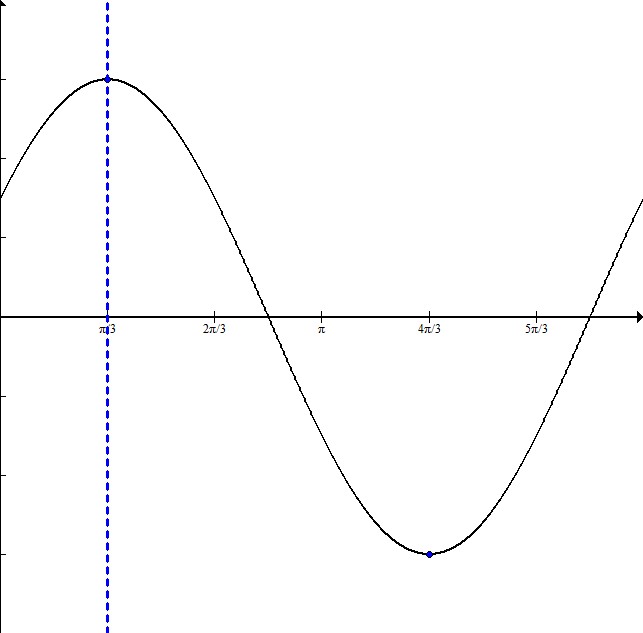
The dotted line is at , where the maximum occurs and therefore where the graph starts. This means that the graph is shifted to the right . 

The distance from the maximum to the minimum is half the entire wavelength. Here it is .

Since half the wavelength is , that means the full wavelength is  so the frequency is just 1.

The amplitude is 3 because the graph goes symmetrically from -3 to 3.

The equation will be in the form  where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift. 

This equation is

.

In the formula,

 .

 represents the phase shift.

Plugging in what we know gives us:

 .

Simplified, the phase is then .

The graph has an amplitude of 2 but has been shifted down 1:

In terms of the equation, this puts a 2 in front of sin, and -1 at the end.

This makes it easier to see that the graph starts [is at 0] where .

The phase shift is  to the right, or . 

The form of the equation will be 

First, think about all possible values of A that could give you an amplitude of 3. Either A = -3 or A = 3 could each produce amplitude = 3. Be sure to look for answer choices that satisfy either of these. 

Secondly, we know that the period is . Normally we know what B is and need to find the period, but this is the other way around. We can still use the same equation and solve:

. You can cross multiply to solve and get B = 4. 

Finally, we need to find a value of C that satisfies 

. Cross multiply to get:

. 

Next, plug in B= 4 to solve for C:

Putting this all together, the equation could either be:

 or 

A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D, 

• amplitude is |A|
• period is 2/|B|
• phase shift is -C/B
• vertical shift is D

In our equation, A=-7, B=6, C=, and D=-4. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift. 

To find amplitude, look at the coefficient in front of the sine function. A=-7, so our amplitude is equal to 7.

The period is 2/B, and in this case B=6. Therefore the period of this function is equal to 2/6 or /3.

To find the phase shift, take -C/B, or -/6. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x. 
6x+=0
6x=-
x=-/6
Either way, our phase shift is equal to -/6.

The vertical shift is equal to D, which is -4.

y=-7\sin(6x+\pi)-4

A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D, 

• amplitude is |A|
• period is 2/|B|
• phase shift is -C/B
• vertical shift is D

In our equation, A=-1, B=1, C=-, and D=3. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift. 

To find amplitude, look at the coefficient in front of the sine function. A=-1, so our amplitude is equal to 1.

The period is 2/B, and in this case B=1. Therefore the period of this function is equal to 2.

To find the phase shift, take -C/B, or . Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x. 
x-=0
x=
Either way, our phase shift is equal to .

The vertical shift is equal to D, which is 3.

A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D, 

• amplitude is |A|
• period is 2/|B|
• phase shift is -C/B
• vertical shift is D

In our equation, A=1, B=2, C=-3, and D=2. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift. 

To find amplitude, look at the coefficient in front of the sine function. A=1, so our amplitude is equal to 1.

The period is 2/B, and in this case B=2. Therefore the period of this function is equal to .

To find the phase shift, take -C/B, or 3/2. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x. 
2x-3=0
2x=3
x=3/2
Either way, our phase shift is equal to 3/2.

The vertical shift is equal to D, which is 2.