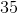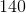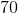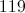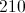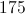The equation for the area of a tirangle is $\displaystyle (Area) =\frac{1}{2}*(Base)*(Height)$

The base in this equation is $\displaystyle 14$ and the height is $\displaystyle 10$ which can be plugged into the formula as:

$\displaystyle (Area) = \frac{1}{2}(14)*(10)$

Finally, we multiply to get:

$\displaystyle (Area) = 70$

The key to solving this problem is remembering what an equilateral triangle is.  In case you forgot, a quick word breakdown will help.  It's easy to see that the first part of the word, "equi" looks an awful lot like equal.  The second part, "lateral", is a little trickier, but we only need to remember that lateral means "side".  In football, a lateral pass is when the player with the ball tosses it to a player on either side.  Putting the two parts together, we see that equilateral just means equal sides.  Therefore an equilateral triangle is a triangle where all three sides have equal length.  That means that if one side of our equilateral triangle has length of $\displaystyle 18cm$, the other two sides are also each $\displaystyle 18cm$ long.

We must also remember that the perimeter of a shape is just the distance around the outside of it.  For our triangle, that means $\displaystyle 18cm$ for the first side, $\displaystyle 18cm$ for the second side, and $\displaystyle 18cm$ for the third side.  That means our perimeter is simply $\displaystyle 18\cdot3=54cm$.

To begin, first find the length of the third side of the triangle. We are given that the two short sides of the triangle have lengths of 5 and 12. Use the Pythagorean Theorem to find the length of the third side:

$\displaystyle \small a^2+b^2=c^2$,

where $\displaystyle \small a$ and $\displaystyle \small b$ represent the two shorter sides of the triangle, and $\displaystyle \small c$ is the hypotenuse:

$\displaystyle \small a^2+b^2=c^2$

$\displaystyle \small \small 5^2+12^2=c^2$

$\displaystyle \small 25+144 = c^2$

$\displaystyle \small 169 = c^2$

$\displaystyle \small \sqrt{169}=\sqrt{c^2}$

$\displaystyle \small c=13$

Now that we have the lengths of all three sides, add them together to find the perimeter:

$\displaystyle \small 5+12+13 = 30$

The perimeter of the triangle is 30.

The correct answer to the question is $\displaystyle 21 ft$.

The formula for finding the perimeter of a triangle is to find the sum of the length of the $\displaystyle 3$ sides. 

The lengths of the three sides of this triangle are $\displaystyle 9 ft$, $\displaystyle 7 ft$, and $\displaystyle 5 ft$. If you add these $\displaystyle 3$ sides, the sum is a perimeter of $\displaystyle 21 ft$.

Using the Pythagorean Theorem, the length of the second leg can be determined.

$\displaystyle a^2+b^2=c^2$

We are given the length of the hypotenuse and one leg.

$\displaystyle a=35, c=91$

$\displaystyle b^2=c^2-a^2\rightarrow b=\sqrt{c^2-a^2}$

$\displaystyle \sqrt{91^{2}-35^{2}} = \sqrt{8,281-1,225} = \sqrt{7,056} = 84$

The perimeter of the triangle is the sum of the lengths of the sides.

$\displaystyle P=35+84+91 = 210$

The perimeter of a shape is the length around the shape. In order to find the perimeter of a triangle, add the lengths of the sides: $\displaystyle 8+12+4=24$.

Because the lengths are in inches, the answer must be in inches as well.

Equilateral triangles have $\displaystyle 3$ sides of equal length. Therefore, by knowing the length of one side, we can calculate the perimeter by multiplying that length by $\displaystyle 3$. 

$\displaystyle 3.5m \times 3 = 10.5 m$

Because the triangle is equilateral, all sidelengths are equal. Thus, if one is 8 they all must be 8, so $\displaystyle 3*8=24$

In an isosceles triangle, two of the three sides are equal to each other.  The possible side lengths of the isosceles are $\displaystyle 3-3-6$ or $\displaystyle 3-6-6$.

The perimeter is the sum of the three sides.

$\displaystyle 3+3+6 = 12$

$\displaystyle 3+6+6 = 15$

The only possible perimeters given the two side lengths are either $\displaystyle 12$ or $\displaystyle 15$.

The correct answer is:  $\displaystyle 12$

There are three equal sides in an equilateral triangle.  

$\displaystyle P=3s$

Substitute the side length.

$\displaystyle P=3\times 5 =15$