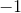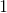Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Operations and Properties

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Add And Subtract Rational Numbers: Ccss.Math.Content.7.Ns.A.1d

Solve:

-2+(-9)+(2-9)

Possible Answers:

Correct answer:

Explanation:

Solve by first combining signs and eliminate the parentheses.

A positive multiplied with a negative sign will give a negative sign.

-2+(-9)+(2-9) = -2-9+2-9 = -18

Report an Error

Example Question #92 : Negative Numbers

Solve:

$-3\times4$

Possible Answers:

Correct answer:

Explanation:

First, since we are multiplying a negative value with a positive value, we need to realize the product is going to be negative. Next, we can multiply the values.

$3\times4=12$

Since the answer is negative, the answer is .

Report an Error

Example Question #1 : Divide Integers: Ccss.Math.Content.7.Ns.A.2b

Solve:

$-90\div-6$

Possible Answers:

Correct answer:

Explanation:

When dividing with two negative values, the answer becomes positive. Then we just divide by , which equals . The answer is +15 or .

Report an Error

Example Question #8 : Divide Integers: Ccss.Math.Content.7.Ns.A.2b

Solve:

$-18\div6$

Possible Answers:

Correct answer:

Explanation:

When dividing with negative numbers, we count the number of negative numbers. We have one so that means the answer is negative. So the quotient is .

Report an Error

Example Question #311 : Operations

Solve:

$-3\left(\frac{-2-6}{-4}\right)$

Possible Answers:

Correct answer:

Explanation:

When solving this problem remember our orders of operation, or PEMDAS.

PEMDAS stands for parentheses, exponents, multiplication/division, and addition/subtraction. When you have a problem with several different operations, you need to solve the problem in this order and you work from left to right for multiplication/division and addition/subtraction.

Simplify the quantities inside the parentheses. Then multiply and distribute the coefficient in front.

$-3\left(\frac{-2-6}{-4}\right)$

$-3\left(\frac{-8}{-4}\right)$

-3(2)=-6

Report an Error

Example Question #93 : Negative Numbers

Solve:

$\frac{-2(2+2)}{-2(-2-2)}$

Possible Answers:

$-\frac{1}{3}$

$\frac{1}{3}$

Correct answer:

Explanation:

When solving this problem remember our orders of operation, or PEMDAS.

Evaluate the quantities inside the parentheses first.

$\frac{-2(2+2)}{-2(-2-2)}$

$\frac{-2(4)}{-2(-4)}$

$\frac{-8}{8}=-1$

Report an Error

Example Question #1 : Absolute Value

Solve:

$\left | -6+4\right |\times7=$

Possible Answers:

Correct answer:

Explanation:

$\left | -6+4\right |\times7=\left | -2\right |\times7=2\times7=14$

Report an Error

Example Question #2 : Absolute Value

Solve:

$\left | 7-3\right |=$

Possible Answers:

Correct answer:

Explanation:

Step 1: solve the problem

$\left | 7-3\right |=\left | 4\right |$

Step 2: solve for absolute value

$\left | 4\right |=4$

Remember, absolute value refers to the total number of units, so it will always be positive. For instance, if I am $4 in debt, I have -$4, but the absolute value of my debt is $4, because that is the total number of dollars that I'm in debt.

Report an Error

Example Question #3 : Absolute Value

Solve:

$\small \small \left | 3-8 \right | =$

Possible Answers:

$\small 11$

$\small -11$

$\small -5$

$\small 5$

Correct answer:

$\small 5$

Explanation:

First, solve the equation:

$\small \left | 3-8 \right | = \left | -5 \right |$

Next, account for the absolute value:

$\small \left | -5 \right | = 5$

Therefore, the answer is $\small 5$ .

Report an Error

Example Question #3 : Absolute Value

Solve the expression below:

$\small \small 19+\left |3*(-6) \right |$

Possible Answers:

$\small -1$

$\small 72$

$\small 1$

$\small 36$

$\small 37$

Correct answer:

$\small 37$

Explanation:

$\small \small \small 19+\left |3*(-6) \right |$ simplifies to $\small \small \small \small 19+\left |-18 \right |$

For absolute value expressions, the value within the bars is treated as positive

So, the expression becomes $\small 19+18$ which adds to $\small 37$

Report an Error

View Pre-Algebra Tutors

Mark
Certified Tutor

View Pre-Algebra Tutors

Tyrone
Certified Tutor

Nova Southeastern University, Bachelor of Science, Computer and Information Sciences, General.

View Pre-Algebra Tutors

Mariam
Certified Tutor

Yarmouk University, Bachelor of Science, Mathematics. Touro College, Master of Science, Teacher Education, Multiple Levels.

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in San Francisco-Bay Area, Spanish Tutors in Denver, English Tutors in Miami, Math Tutors in Phoenix, Computer Science Tutors in Phoenix, Biology Tutors in Dallas Fort Worth, SSAT Tutors in New York City, ISEE Tutors in Dallas Fort Worth, ISEE Tutors in Los Angeles, GRE Tutors in Phoenix

Popular Courses & Classes

ACT Courses & Classes in Philadelphia, ISEE Courses & Classes in Chicago, SSAT Courses & Classes in Chicago, MCAT Courses & Classes in Chicago, SAT Courses & Classes in Phoenix, SSAT Courses & Classes in Seattle, ISEE Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Miami, ACT Courses & Classes in Chicago, SSAT Courses & Classes in San Diego

Popular Test Prep

MCAT Test Prep in San Diego, ACT Test Prep in Denver, SSAT Test Prep in Denver, GRE Test Prep in Boston, SSAT Test Prep in Chicago, ACT Test Prep in Atlanta, LSAT Test Prep in Houston, MCAT Test Prep in Philadelphia, ISEE Test Prep in Chicago, SSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Operations and Properties

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #3 : Add And Subtract Rational Numbers: Ccss.Math.Content.7.Ns.A.1d

Example Question #92 : Negative Numbers

Example Question #1 : Divide Integers: Ccss.Math.Content.7.Ns.A.2b

Example Question #8 : Divide Integers: Ccss.Math.Content.7.Ns.A.2b

Example Question #311 : Operations

Example Question #93 : Negative Numbers

Example Question #1 : Absolute Value

Example Question #2 : Absolute Value

Example Question #3 : Absolute Value

Example Question #3 : Absolute Value

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: