All Pre-Algebra Resources
Example Questions
Example Question #1 : Number Theory
Which number is the reciprocal of the reciprocal of ?
The reciprocal of the reciprocal of any number is the original number. Therefore, the correct choice is .
Example Question #2 : Number Theory
Order the following numbers from least to greatest.
The main obstacle to solving this problem is the fact that two of the numbers are expressed as fractions while the other two are written as decimals. That means that before we can order them, it might be easiest to change the numbers to either all fractions or all decimals. Changing the fractions to decimals will prove the easier route. You can do this using a calculator by simply dividing the numerator by the denominator. If you do not have a calculator or cannot use one, long division will accomplish the same end. Dividing 3 by 4 in the first fraction results in the decimal . Dividing 7 by 9 in the second fractions becomes slightly more complicated. If you used, a calculator, the screen probably lists something to the effect of , with the number of sevens before the eight depending on how many digits your calculator displays. If you used long division, you will just keep getting 7 over and over again for the next digit with no end in sight. Both answers are correct, as 7 divided by 9 will result in an endless line of sevens after the decimal point. The reason the calculator included an 8 at the end was because it ran out of space. Like a good calculator, it decided to round based on the next digit after the last one that would fit. Since that digit would also be a 7, the calculator rounds the last digit on the screen up to an 8.
In math we denote a repeating decimal like this one by putting a bar over the portion that repeats. In other words,
That means that one of the other decimals from our original list is also repeating. Notice that in the bar only covers the 5 and not the 7 as well. That means only the 5 repeats, such that
Knowing this we are now able to look at each of the numbers as a decimal. In the number , the digits following the 7 are technically all zeroes.
Therefore, all of the numbers have a 7 in the tenths place (the first place after the decimal), but has the smallest hundredths place (the second place after the decimal), making it the smallest.
, which we changed to , follows the same principle. It's thousandths place (third after the decimal) would be a 0, as would each of the following.
Therefore, even though also has a 5 in the hundredths place, its thousandths place is a 5, making the smaller of the two numbers and the second smallest overall.
Since , it's hundreths place is also a 7, making it larger than the others. We now have our order.
Example Question #2 : Number Theory
Which of the following are real numbers
b and c
a and c
a and b
All of the above
c and d
a and c
a) can be solved and written as which is a real number.
b) is not a real number. The reason is that there is no real number which can multiply by itself to give a negative number.
c) can be written as which can be simplified as which is a real number.
d) Infinity is an imaginary number. So, not a real number.
Hence the answer is a and c.
Example Question #1 : Real Numbers
If is a real number, which of the following CANNOT be a value for x?
-3
122
125
3
-122
3
The definition of the set of real numbers is the set of all numbers that can fit into a/b where a and b are both integers and b does not equal 0.
So, since we see a fraction here, we know a non-real number occurs if the denominator is 0. Therefore we can find where the denominator is 0 by setting x-3 =0 and solving for x. In this case, x=3 would create a non-real number. Thus our answer is that x CANNOT be 3 for our expression to be a real number.
Example Question #1 : Real Numbers
If are both negative, then could NOT be equal to....
is negative and is positive
Therefore, the solution cannot be negative.
Example Question #1 : Number Theory
If is a real number, which one of these cannot be a value of ?
For the expression to be defined, the denominator needs to be different from 0. Therefore:
So the correct answer is 2.
Example Question #3 : Real Numbers
If is a real number, which of the following cannot be a value of ?
In order to be a real number, must be positive, since the square root of a negative number is not a real number. So we have to find the answer choice that makes negative:
Therefore, the correct answer is .
Example Question #2 : Number Theory
Which answer provides a set of real numbers?
All of the above
All of the above
All rational and irrational numbers are considered real numbers, therefore the correct answer is:
All of the above
Example Question #2 : Real Numbers
Which of the following is a real number?
All of them.
All of them.
A real number is considered the union of the sets of rational numbers and irrational numbers. A real number can be positive, negative, fractions, whole numbers, decimals, irrational numbers, etc. Therefore, all of the numbers mentioned are real numbers.
Example Question #3 : Number Theory
Which of the following is an integer and is not a whole number?
An integer is any number without a fractional component, such as the following:
A whole number is any positive number with no fractional component, such as the following:
The major difference between the two groups of numbers is that there are no negative whole numbers, while there are negative integers.
The first step of this problem is to eliminate any choices that are not integers. The choices , , and , are all fractions or contain fractional components, so none of these values can be considered integers.
Of the remaining choices, falls under the categories of whole number and integer, so it cannot be the answer.
fufills both requirements of the question. It is an integer by having no fractional component, and it is not a whole number because it is a negative value, so it must be the correct answer.
All Pre-Algebra Resources











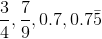














































![x^3 = 8 \Leftrightarrow x = \sqrt[3]{8} \Leftrightarrow x = (2^{3})^{\frac{1}{3}} = 2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/266197/gif.latex)






































