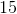When two negative values are multiplied, the answer becomes positive. Then, we multiply normally. We should get  or .

Remember PEMDAS. The parentheses comes first. When adding a negative value, the operation is subtraction. We now have . The answer in the parentheses is , but since there is a negative sign outside, we need to add that in so final answer becomes . 

To determine the answer, it's best to compare the values without doing any math. Since  is bigger than  and the  has the positive sign in front, the answer is positive. Also, with addition, you can rewrite the expression without altering the answer. So, instead we can write . The positive and negative value combined gives us a negative sign and now we have  or . 

When given multiple operations, remember PEMDAS. Division comes before subtraction. So we divide  by  first to get an answer of . Now we have an expression of . To determine the answer, it's best to compare the values without doing any math. Since  is bigger than  and the  has the negative sign in front, the answer is negative. So, just subtract  with  to get . Since the answer should be negative, the final answer is . 

When multiplying with multiple signs involved, count the number of positive and negative signs. There are  negative values and  positive values. Since there are more negatiive values, the answer should be negative. When we multiply out the expression, we get . But our answer should be negative because there were more negative values than positive vaules, so our answer is . 

Remember PEMDAS. The parentheses comes first so let's work what's inside. When adding a negative sign, the operation becomes negative. So, we have . To determine the answer, it's best to compare the values without doing any math. Since  is bigger than  and the  has the negative sign in front, the answer is negative. So, we subtract normally to get  but the actual answer should be . Now, we hae . Two negatives make a positive so the final answer is . 

Remember PEMDAS. Let's work the parantheses first. For  we have opposite signs in the product so the answer should be negative.  is . Next, on the last parantheses, . First we will do . When multiplying two negatives, we get a positive value.  is . Next, we need to divide  by .  When that positive value is divided by a negative value, the answer is negative. So  is Now, we have:

. We can now work from left to right. When adding positive with negative, the sign becomes negative. Since  is greater than  and it's negative, the expression becomes subtraction. We get . Next, with two negative signs, we get a positive value. The expression is now . We can add all the positive values and get an expression of . Since  is greater than  and  is positive, the answer is positive. We treat this as a subtraction problem because of the  and the difference is . The answer we want is positive so the answer is still . 

Remember PEMDAS. The parantheses come first. On the left we have  is greater than  and it's negative. We turn that expression into a subtraction problem and get  in the first paranthesis. On the other parentheses, two negatives make a positive so now it becomes  or . Now we have . Now we can work left to right. On the left, since we are multiplying two negative values, the answer is positive. So we have  or . On the right, with opposite signs, we get a negative answer. So that becomes . Now we have . Since we are dividing opposite signs, the answer is negative. The quotient is  but we want a negative value so final answer is . 

When we subtract a negative number, the sign turns positive. It becomes an addition problem. .

When multiplying with negative numbers, we count the number of negative numbers. We have two so that means the answer is positive. So the product is .