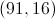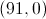Pre-Algebra : Graphing
Study concepts, example questions & explanations for Pre-Algebra
All Pre-Algebra Resources
Example Questions
Example Question #12 : Graphing Points
Write the ordered pair of points a, b, and c.
An ordered is always written in the following format:
where x is the position on the x-axis, and y is the position on the y-axis.
If we look at point a, we find where it falls on the x-axis. We can see that it's position on the x-axis is 1. Then, we see where it falls on the y-axis. It's position on the y-axis is 4. So, we can write the ordered pair for point a as
We will do the same for b. The position of point b on the x-axis is -5. The position of point b on the y-axis is 2. So, we can write the ordered pair for point b as
And finally for c. The position of point c on the x-axis is zero. The position of point c on the y-axis is -5. So, we can write the ordered pair of point c as
Example Question #13 : Graphing Points
Which of the following points is found in the second quadrant of a coordinate plane?
The following coordinate plane displays the different quandrants.
You can also see there is a point that has been graphed.
That point is (-3, 4).
Therefore, (-3, 4) can be found in the second quandrant of a coordinate plane.
Example Question #14 : Graphing Points
Find the midpoint of the following points:
(-5, 6) and (1, 2)
The midpoint formula is
where 
(-5, 6) and (1, 2) we can substitute into the midpoint formula and get
Therefore, the midpoint is (-2, 4).
Example Question #15 : Graphing Points
Which quadrant does the coordinates 
When looking at a coordinate plane, draw the letter C in there making sure you connect all four quarters of the grid. The C should start in the top right corner, move to the top left, then bottom left, then finish in the bottom right corner.
The quadrants start with 
Therefore the coordinates 
Example Question #1 : Graphing Lines
What is the slope of the line with the equation 
In the standard form equation of a line, 
In this case the line 
Therefore the answer is 
Example Question #2 : Graphing Lines
What is the slope of the line that contains the points
To find the slope of a line with two points you must properly plug the points into the slope equation for two points which is
We must then properly assign the points to the equation as 
In this case we will make 
Plugging the points into the equation yields
Perform the math to arrive at
The answer is 
Example Question #1 : How To Graph A Line In Pre Algebra
What is the slope of the line 
In the standard form of a line 
In this case the line 
The answer is 
Example Question #3 : Graphing Lines
The equation of a line is 
What are the slope and the y-intercept?
Slope:
y-intercept:
Slope:
y-intercept:
Slope:
y-intercept:
Slope:
y-intercept:
Slope:
y-intercept:
The equation of the line is written in slope-intercept form, 
Example Question #1 : How To Graph A Point In Pre Algebra
What is the y-intercept of the line 
The y-intercept is the point at which the line intersects the y-axis.
It does this at 
We plug 
Anything multiplied by 
Our coordinates for the y-intercept are 
Example Question #2 : Graphing Lines
What is the slope of the line 
In the slope-intercept form of a line,
In this case the line
has a slope of 
The answer is 
Certified Tutor
Certified Tutor
All Pre-Algebra Resources
