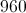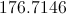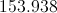Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Area

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : Area Of A Circle

A circle has a diameter of inches. What is the area of the circle? Round to the nearest tenth decimal place.

Possible Answers:

$56.7 \textup{ in}^2$

$75.4 \textup{ in}^2$

$314.3 \textup{ in}^2$

$78.5 \textup{ in}^2$

$45.8 \textup{ in}^2$

Correct answer:

$78.5 \textup{ in}^2$

Explanation:

The formula to find the area of a circle is $A=\pi\cdot r^2$ .

First you must find the radius from the diameter.

$r=\frac{1}{2}d \rightarrow r=\frac{1}{2}\cdot 10=5$

In this case it is,

$A=5^2 \cdot \pi = 25\cdot 3.14= 78.5$

Report an Error

Example Question #1 : Area Of A Circle

What is the area of a circle that has a diameter of inches?

Possible Answers:

706.8583

153.938

176.7146

940

153.938

940

960

Correct answer:

176.7146

Explanation:

The formula for finding the area of a circle is $\pi r^{2}$ . In this formula, represents the radius of the circle. Since the question only gives us the measurement of the diameter of the circle, we must calculate the radius. In order to do this, we divide the diameter by .

$\frac{15}{2}=7.5$

Now we use 7.5 for in our equation.

$\pi (7.5)^{2}=176.7146 \: in^{2}$

Report an Error

Example Question #3 : Area Of A Circle

What is the area of a circle with a diameter equal to 6?

Possible Answers:

$18\pi$

$36\pi$

$9\pi$

$3\pi$

Correct answer:

$9\pi$

Explanation:

First, solve for radius:

$r=\frac{d}{2}=\frac{6}{2}=3$

Then, solve for area:

$A=r^2\pi=3^2\pi=9\pi$

Report an Error

Example Question #1 : Area Of A Circle

The diameter of a circle is $4\ cm$ . Give the area of the circle.

Possible Answers:

$13.56\ cm^2$

$12 \ cm^2$

$13\ cm^2$

$12.56\ cm^2$

$11.56\ cm^2$

Correct answer:

$12.56\ cm^2$

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle, and $\pi$ is approximately 3.14 .

$Area=\frac{\pi d^2}{4}=\frac{\pi\times 4^2}{4}=4\pi \Rightarrow Area\approx 4\times 3.14\Rightarrow Area\approx 12.56 \ cm^2$

Report an Error

Example Question #171 : Isee Upper Level (Grades 9 12) Mathematics Achievement

The diameter of a circle is . Give the area of the circle in terms of .

Possible Answers:

12.56 t^2

11.56 t^2

12 t^2

12.56 t

11.56 t

Correct answer:

12.56 t^2

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle and $\pi$ is approximately 3.14 .

$Area=\frac{\pi (4t)^2}{4}=\frac{16\pi t^2}{4}=4\pi t^2 \Rightarrow Area\approx 4\times 3.14\times t^2$

$\Rightarrow Area\approx 12.56t^2$

Report an Error

Example Question #5 : Area Of A Circle

The circumference of a circle is 12.56 inches. Find the area of the circle.

Let $\pi = 3.14$ .

Possible Answers:

$11.56\ in^2$

$11\ in^2$

$13.56\ in^2$

$12.56\ in^2$

$12\ in^2$

Correct answer:

$12.56\ in^2$

Explanation:

First we need to find the radius of the circle. The circumference of a circle is $Circumference =2\pi r$ , where is the radius of the circle.

$12.56=2\times 3.14\times r\Rightarrow r=2\ in$

The area of a circle is $Area=\pi r^2$ where is the radius of the circle.

$Area=\pi r^2=3.14\times 2^2=12.56\ in^2$

Report an Error

Example Question #122 : Area

Find the area of a circle that has a radius of .

Possible Answers:

$16\pi$

$12\pi$

$4\pi$

$8\pi$

Correct answer:

$16\pi$

Explanation:

Use the formula:

$\text{Area}=\pi\times r^2$

Where corresponds to the circle's radius.

Since r=4 :

$\text{Area}=\pi\times(4^2)$

$\text{Area}=16\pi$

Report an Error

Example Question #121 : Area

Find the area of a circle that has a radius of .

Possible Answers:

$4x\pi$

$x\pi$

$2x\pi$

$x^2\pi$

Correct answer:

$x^2\pi$

Explanation:

Use the formula:

$\text{Area}=\pi\times r^2$

Where corresponds to the circle's radius.

Since r=x :

$\text{Area}=\pi\times(x^2)$

$\text{Area}=x^2\pi$

Report an Error

Example Question #122 : Area

Find the area of a circle that has a radius of .

Possible Answers:

$17\pi$

$34\pi$

$128\pi$

$289\pi$

Correct answer:

$289\pi$

Explanation:

Use the formula:

$\text{Area}=\pi\times r^2$

Where corresponds to the circle's radius.

Since r=17 :

$\text{Area}=\pi\times(17^2)$

$\text{Area}=289\pi$

Report an Error

Example Question #123 : Area

Find the area of a circle with a diameter of .

Possible Answers:

$36\pi$

$12\pi$

$24\pi$

$144\pi$

Correct answer:

$36\pi$

Explanation:

Use the formula:

$\text{Area}=\pi\times r^2$

Where corresponds to the circle's radius.

We were given the circle's diameter, .

d=2r

Substitute.

12=2r

Divide both sides by .

$\frac{12}{2}=r$

r=6

Solve for the area of the circle.

$\text{Area}=\pi\times(6^2)$

$\text{Area}=36\pi$

Report an Error

View Pre-Algebra Tutors

Jacqueline
Certified Tutor

Yale University, Bachelor of Science, German Studies. Cornell University, Master of Science, German Studies.

View Pre-Algebra Tutors

Varun
Certified Tutor

Saint Louis University-Main Campus, Bachelor of Science, Neuroscience. Saint Louis University-Main Campus, Doctor of Medicine...

View Pre-Algebra Tutors

Leonard
Certified Tutor

Sam Houston State University, Bachelor of Science, Criminal Justice. Louisiana State University-Alexandria, Masters in Busine...

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Washington DC, English Tutors in Phoenix, Reading Tutors in Seattle, SAT Tutors in Denver, GRE Tutors in Dallas Fort Worth, GRE Tutors in Miami, Algebra Tutors in Seattle, ISEE Tutors in Phoenix, ACT Tutors in Los Angeles, SSAT Tutors in Washington DC

Popular Courses & Classes

ISEE Courses & Classes in Seattle, SSAT Courses & Classes in Boston, ACT Courses & Classes in Seattle, SSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Washington DC, ACT Courses & Classes in New York City, SAT Courses & Classes in Chicago, ACT Courses & Classes in Denver, SSAT Courses & Classes in San Diego, Spanish Courses & Classes in Los Angeles

Popular Test Prep

ACT Test Prep in Denver, GRE Test Prep in New York City, ISEE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Miami, MCAT Test Prep in Miami, SAT Test Prep in Phoenix, GRE Test Prep in Philadelphia, ACT Test Prep in Atlanta, SSAT Test Prep in Atlanta, ISEE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Area

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #4 : Area Of A Circle

Example Question #1 : Area Of A Circle

Example Question #3 : Area Of A Circle

Example Question #1 : Area Of A Circle

Example Question #171 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #5 : Area Of A Circle

Example Question #122 : Area

Example Question #121 : Area

Example Question #122 : Area

Example Question #123 : Area

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: