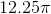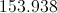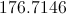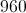Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Area of a Circle

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Area Of A Circle

A circle has a circumference of $\small 6\pi$ . What is its area?

Possible Answers:

$\small 9\pi$

$\small 6\pi$

$\small 12\pi$

$\small 18\pi$

$\small 36\pi$

Correct answer:

$\small 9\pi$

Explanation:

To begin, we need to find the radius of the circle. The circumference of a circle is given as follows:

$\small C = 2\pi r$ ,

where is the radius.

Then, a circle with circumference $6\pi$ will have the following radius:

$6\pi = 2\pi r$

$\small \frac{6\pi}{2\pi}=\frac{2\pi r}{2\pi}$

$\small 3=r$

Using the radius, we can now solve for the area:

$\small A=\pi r^2$

$A=\pi(3)^2$

$\small A=9\pi$

The area of the circle is $\small 9\pi$ .

Report an Error

Example Question #2 : Area Of A Circle

What is the area of a circle with a diameter equal to ?

Possible Answers:

$12.25\pi$

$49\pi$

$24.5\pi$

$98\pi$

Correct answer:

$12.25\pi$

Explanation:

If the diameter is 7, then the radius is half of 7, or 3.5.

Plug this value for the radius into the equation for the area of a circle:

$A=r^2\pi=(3.5)^2\pi=12.25\pi$

Report an Error

Example Question #2 : Area Of A Circle

Untitled_1

The rectangle in the above figure has length 20 and height 10. What is the area of the orange region?

Possible Answers:

$200 + 100 \pi$

$200 + 50 \pi$

$200 + \frac{25}{2} \pi$

$200 + 25 \pi$

Insufficient information is given to determine the area.

Correct answer:

$200 + \frac{25}{2} \pi$

Explanation:

The orange region is a composite of two figures:

One is a rectangle measuring 20 by 10, which, subsequently, has area

$20 \cdot 10 = 200$ .

The other is a semicircle with diameter 10, and, subsequently, radius 5. Its area is

$\frac{1}{2} \pi \cdot 5^{2} = \frac{25}{2} \pi$ .

Add the areas:

$A = 200 + \frac{25}{2} \pi$

Report an Error

Example Question #3 : Area Of A Circle

A circle has a diameter of inches. What is the area of the circle? Round to the nearest tenth decimal place.

Possible Answers:

$314.3 \textup{ in}^2$

$45.8 \textup{ in}^2$

$75.4 \textup{ in}^2$

$78.5 \textup{ in}^2$

$56.7 \textup{ in}^2$

Correct answer:

$78.5 \textup{ in}^2$

Explanation:

The formula to find the area of a circle is $A=\pi\cdot r^2$ .

First you must find the radius from the diameter.

$r=\frac{1}{2}d \rightarrow r=\frac{1}{2}\cdot 10=5$

In this case it is,

$A=5^2 \cdot \pi = 25\cdot 3.14= 78.5$

Report an Error

Example Question #1 : Area Of A Circle

What is the area of a circle that has a diameter of inches?

Possible Answers:

940

706.8583

960

176.7146

153.938

Correct answer:

176.7146

Explanation:

The formula for finding the area of a circle is $\pi r^{2}$ . In this formula, represents the radius of the circle. Since the question only gives us the measurement of the diameter of the circle, we must calculate the radius. In order to do this, we divide the diameter by .

$\frac{15}{2}=7.5$

Now we use 7.5 for in our equation.

$\pi (7.5)^{2}=176.7146 \: in^{2}$

Report an Error

Example Question #1 : Area Of A Circle

What is the area of a circle with a diameter equal to 6?

Possible Answers:

$3\pi$

$9\pi$

$36\pi$

$18\pi$

Correct answer:

$9\pi$

Explanation:

First, solve for radius:

$r=\frac{d}{2}=\frac{6}{2}=3$

Then, solve for area:

$A=r^2\pi=3^2\pi=9\pi$

Report an Error

Example Question #931 : Grade 7

The diameter of a circle is $4\ cm$ . Give the area of the circle.

Possible Answers:

$12.56\ cm^2$

$12 \ cm^2$

$11.56\ cm^2$

$13.56\ cm^2$

$13\ cm^2$

Correct answer:

$12.56\ cm^2$

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle, and $\pi$ is approximately 3.14 .

$Area=\frac{\pi d^2}{4}=\frac{\pi\times 4^2}{4}=4\pi \Rightarrow Area\approx 4\times 3.14\Rightarrow Area\approx 12.56 \ cm^2$

Report an Error

Example Question #4 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

The diameter of a circle is . Give the area of the circle in terms of .

Possible Answers:

11.56 t

12.56 t^2

11.56 t^2

12.56 t

12 t^2

Correct answer:

12.56 t^2

Explanation:

The area of a circle can be calculated using the formula:

$Area=\frac{\pi d^2}{4}$ ,

where is the diameter of the circle and $\pi$ is approximately 3.14 .

$Area=\frac{\pi (4t)^2}{4}=\frac{16\pi t^2}{4}=4\pi t^2 \Rightarrow Area\approx 4\times 3.14\times t^2$

$\Rightarrow Area\approx 12.56t^2$

Report an Error

Example Question #1 : Area Of A Circle

The circumference of a circle is 12.56 inches. Find the area of the circle.

Let $\pi = 3.14$ .

Possible Answers:

$11\ in^2$

$12\ in^2$

$13.56\ in^2$

$12.56\ in^2$

$11.56\ in^2$

Correct answer:

$12.56\ in^2$

Explanation:

First we need to find the radius of the circle. The circumference of a circle is $Circumference =2\pi r$ , where is the radius of the circle.

$12.56=2\times 3.14\times r\Rightarrow r=2\ in$

The area of a circle is $Area=\pi r^2$ where is the radius of the circle.

$Area=\pi r^2=3.14\times 2^2=12.56\ in^2$

Report an Error

Example Question #5 : Area Of A Circle

Find the area of a circle that has a radius of .

Possible Answers:

$4\pi$

$16\pi$

$12\pi$

$8\pi$

Correct answer:

$16\pi$

Explanation:

Use the formula:

$\text{Area}=\pi\times r^2$

Where corresponds to the circle's radius.

Since r=4 :

$\text{Area}=\pi\times(4^2)$

$\text{Area}=16\pi$

Report an Error

View Pre-Algebra Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View Pre-Algebra Tutors

Priyanvada
Certified Tutor

University of North Texas, Doctor of Philosophy, Materials Engineering.

View Pre-Algebra Tutors

Jeffrey
Certified Tutor

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Chicago, Biology Tutors in Chicago, Computer Science Tutors in Miami, Algebra Tutors in Boston, Calculus Tutors in Chicago, GMAT Tutors in Phoenix, Math Tutors in Washington DC, GRE Tutors in Washington DC, ACT Tutors in Philadelphia, ACT Tutors in San Diego

Popular Courses & Classes

LSAT Courses & Classes in Miami, ACT Courses & Classes in Philadelphia, GRE Courses & Classes in San Diego, LSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in San Diego, GMAT Courses & Classes in Atlanta, GMAT Courses & Classes in Chicago, Spanish Courses & Classes in Washington DC, ISEE Courses & Classes in Houston, SAT Courses & Classes in Denver

Popular Test Prep

SSAT Test Prep in Los Angeles, GMAT Test Prep in Miami, ACT Test Prep in Philadelphia, SAT Test Prep in Denver, GMAT Test Prep in New York City, ISEE Test Prep in Chicago, MCAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Atlanta, SAT Test Prep in Boston, GRE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Area of a Circle

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #1 : Area Of A Circle

Example Question #2 : Area Of A Circle

Example Question #2 : Area Of A Circle

Example Question #3 : Area Of A Circle

Example Question #1 : Area Of A Circle

Example Question #1 : Area Of A Circle

Example Question #931 : Grade 7

Example Question #4 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4

Example Question #1 : Area Of A Circle

Example Question #5 : Area Of A Circle

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: