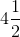Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Two-Step Equations

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #111 : Algebraic Equations

Solve for .

4x + 12 = 8

Possible Answers:

x = -1

x = 5

x = 1

x = -2

x = 2

Correct answer:

x = -1

Explanation:

When solving for x, we must get x to be by itself. So,

4x + 12 = 8

we subtract 12 from both sides. We get,

4x + 12 - 12 = 8 - 12

4x = -4

Now, we divide both sides by 4. We get

$\frac{4x}{4} = \frac{-4}{4}$

x = -1

Report an Error

Example Question #121 : Algebraic Equations

Solve for x in the following equation:

$\frac{x}{6} + 3 = -3$

Possible Answers:

x = -1

x = -6

x = 0

x = 6

x = -36

Correct answer:

x = -36

Explanation:

When solving for x, we want to get x to stand alone. So in the equation

$\frac{x}{6} + 3 = -3$

we first subtract 3 from both sides.

$\frac{x}{6} + 3 - 3 = -3 - 3$

$\frac{x}{6} = -6$

Now, we multiply by 6 on both sides.

$\frac{x}{6} \cdot 6 = -6 \cdot 6$

x = -36

Report an Error

Example Question #61 : Two Step Equations With Integers

Solve for x:

-x+2=0

Possible Answers:

None of the above

Correct answer:

Explanation:

The first step in this equation is to bring the 2 over to the other side by subtraction so you will get:

-x=-2

then you need to divide by negative one to get a positive "x."

Your final answer is

x=2

Report an Error

Example Question #1 : Two Step Equations With Fractions

Solve for :

$\frac{1}{2}x+\frac{3}{4}=9$

Possible Answers:

$16\frac{1}{2}$

$4\frac{1}{2}$

$16\frac{3}{4}$

$16\frac{1}{4}$

Correct answer:

$16\frac{1}{2}$

Explanation:

The goal is to isolate the variable on one side.

$\frac{1}{2}x+\frac{3}{4}=9$

Subtract $\frac{3}{4 }$ from each side of the equation:

$\frac{1}{2}x+\frac{3}{4}-\frac{3}{4}=9-\frac{3}{4}$

$\frac{1}{2}x=8\frac{1}{4}$

Multiply both sides by :

$x=16\frac{1}{2}$

Report an Error

Example Question #123 : Algebraic Equations

Solve for :

$\frac{2}{3}x+6\frac{1}{3}=10\frac{1}{3}$

Possible Answers:

Correct answer:

Explanation:

The goal is to isolate the variable to one side.

$\frac{2}{3}x+6\frac{1}{3}=10\frac{1}{3}$

First, convert mixed numbers to improper fractions:

$\frac{2}{3}x+\frac{19}{3}=\frac{31}{3}$

Subtract $\frac{19}{3}$ from both sides:

$\frac{2}{3}x+\frac{19}{3}-\frac{19}{3}=\frac{31}{3}-\frac{19}{3}$

$\frac{2}{3}x=\frac{12}{3}$

Multiply each side by the reciprocal of $\frac{2}{3}$ :

$\frac{3}{2}*\frac{2}{3}x=\frac{12}{3}*\frac{3}{2}$

Cross out like terms and multiply:

$\frac{1}{1}x=\frac{6}{1}*\frac{1}{1}$

x=6

Report an Error

Example Question #2 : Two Step Equations With Fractions

Solve for :

$\frac{2}{3}x-\frac{1}{4}=\frac{1}{6}$

Possible Answers:

$\frac{5}{12}$

$\frac{5}{8}$

$-\frac{1}{8}$

$-\frac{1}{18}$

$\frac{5}{18}$

Correct answer:

$\frac{5}{8}$

Explanation:

Step 1: Add $\frac{1}{4}$ to both sides:

$\frac{2}{3}x-\frac{1}{4}+\frac{1}{4}=\frac{1}{6}+\frac{1}{4}$

$\frac{2}{3}x+0=\frac{1}{6}+\frac{1}{4}$

$\frac{2}{3}x=\frac{1}{6}+\frac{1}{4}$

Step 2: Add $\frac{1}{6}$ to $\frac{1}{4}$ . Remember that when you add fractions, you must find common denominator. The common denominator for $\frac{1}{4}$ and $\frac{1}{6}$ is . $\frac{1}{6}$ becomes $\frac{2}{12}$ when you multiply both the numerator and the denominator by . Similarly, $\frac{1}{4}$ becomes $\frac{3}{12}$ when you multiply both the numerator and the denominator by .

$\frac{2}{3}x=\frac{1}{6}+\frac{1}{4}$

$\frac{2}{3}x=\frac{2}{12}+\frac{3}{12}$

$\frac{2}{3}x=\frac{5}{12}$

Step 3: Multiply both sides of the equation by the reciprocal of $\frac{2}{3}$ :

$\frac{3}{2}\times \frac{2}{3}x=\frac{5}{12}\times \frac{3}{2}$

$1x=\frac{15}{24}$

$x=\frac{15}{24}$

Step 4: Simplify the fraction by dividing the numerator and the denominator by the Greatest Common Factor (GCF). The GCF of and is :

$x=\frac{15}{24}=\frac{\frac{15}{3}}{\frac{24}{3}}=\frac{5}{8}$

$x=\frac{5}{8}$

Report an Error

Example Question #3 : Two Step Equations With Fractions

Solve for $\small x$ :

$\frac{1}{2}x+2=4$

Possible Answers:

$\small 4$

$\small 8$

$\small 6$

$\small 1$

$\small 2$

Correct answer:

$\small 4$

Explanation:

You are trying to isolate the $\small x$ .

To do this you must first subtract both sides by 2 to get

$\frac{1}{2}x=2$

This then becomes a one-step problem where you multiply both sides by 2 to get

x=4

Report an Error

Example Question #2 : Two Step Equations With Fractions

Solve for x:

$x-\frac{1}{4}=\frac{1}{2}$

Possible Answers:

$x=-\frac{1}{4}$

$x=\frac{3}{4}$

$x=\frac{3}{2}$

$x=\frac{3}{8}$

x=1

Correct answer:

$x=\frac{3}{4}$

Explanation:

Once you've isolated x, it's important to find the lowest common denominator so that you can add the two fractions you're working with.

Step 1: Isolate x and convert fractions so that they have a common denominator

$x-\frac{1}{4}+\frac{1}{4}=\frac{1}{2}+\frac{1}{4}$

$x=\frac{1}{2}+ \frac{1}{4}=\frac{1\cdot 2}{2\cdot 2} +\frac{1}{4}=\frac{2}{4}+\frac{1}{4}$

Step 2: solve for x

$x=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}, x=\frac{3}{4}$

Report an Error

Example Question #3 : Two Step Equations With Fractions

Solve for .

$\frac{x}4=\frac{9}x{}{}$

Possible Answers:

$x=\frac{4}9{}$

$x=\frac{36}x{}$

$x=\pm \frac{3}2{}$

x=36

$x=\pm 6$

Correct answer:

$x=\pm 6$

Explanation:

Cross multiplication is a short-cut that comes from multiplying by the denominators on both sides of an equation. Broken down, it works like this:

$4\cdot \frac{x}4=\frac{9}x\cdot 4{}{}$

The 4's on the left side of the equation cancel out.

$x=\frac{9\cdot 4}x{}$

Now, do the same with the denominator on the right side.

$x\cdot x=\frac{9\cdot 4}x\cdot x{}$

The 's on the right cancel out.

$x\cdot x=9\cdot 4$

This is simply the result of removing the denominators, then multiplying them on the opposite sides, i.e. cross multiplication.

Now, to finish solving for , simplify both sides.

$x^{2}=36$

Then take the square root to finish.

$x=\sqrt{36}$

$x=\pm 6$

Report an Error

Example Question #6 : Two Step Equations With Fractions

Solve for :

$\frac{2}{3}s+\frac{1}{3}=-\frac{1}{3}$

Possible Answers:

s=2

s=1

s=-1

s=0

Correct answer:

s=-1

Explanation:

$\frac{2}{3}s+\frac{1}{3}=-\frac{1}{3}$

$\frac{2}{3}s+\frac{1}{3}-\frac{1}{3}=-\frac{1}{3}-\frac{1}{3}$

$\frac{2}{3}s=-\frac{2}{3}$

$\frac{3}{2}\cdot \left(\frac{2}{3}s\right)=\frac{3}{2}\cdot \left(-\frac{2}{3}\right)$

s=-1

Report an Error

View Pre-Algebra Tutors

Priyanvada
Certified Tutor

University of North Texas, Doctor of Philosophy, Materials Engineering.

View Pre-Algebra Tutors

Emmanuel
Certified Tutor

Baylor University, Bachelor of Science, Biology, General.

View Pre-Algebra Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Philadelphia, Chemistry Tutors in Dallas Fort Worth, Algebra Tutors in Boston, Math Tutors in Houston, Chemistry Tutors in San Diego, Math Tutors in San Francisco-Bay Area, Computer Science Tutors in Seattle, ACT Tutors in Chicago, Math Tutors in Denver, French Tutors in Washington DC

Popular Courses & Classes

GMAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Seattle, ACT Courses & Classes in Los Angeles, SAT Courses & Classes in Miami, SAT Courses & Classes in Los Angeles, GMAT Courses & Classes in New York City, Spanish Courses & Classes in Philadelphia, ACT Courses & Classes in New York City, MCAT Courses & Classes in Boston, LSAT Courses & Classes in San Diego

Popular Test Prep

SAT Test Prep in Los Angeles, SSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Philadelphia, ACT Test Prep in Los Angeles, ISEE Test Prep in San Diego, GMAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Boston, SSAT Test Prep in Seattle, LSAT Test Prep in Washington DC, ACT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Two-Step Equations

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #111 : Algebraic Equations

Example Question #121 : Algebraic Equations

Example Question #61 : Two Step Equations With Integers

Example Question #1 : Two Step Equations With Fractions

Example Question #123 : Algebraic Equations

Example Question #2 : Two Step Equations With Fractions

Example Question #3 : Two Step Equations With Fractions

Example Question #2 : Two Step Equations With Fractions

Example Question #3 : Two Step Equations With Fractions

Example Question #6 : Two Step Equations With Fractions

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: