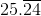Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Two-Step Equations

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #22 : Two Step Equations With Fractions

Solve: $\frac{1}{2}x -\frac{7}{8} = \frac{15}{8}$

Possible Answers:

$\frac{11}{2}$

$\frac{2}{11}$

$\frac{11}{16 }$

$\frac{16 }{11}$

Correct answer:

$\frac{11}{2}$

Explanation:

In order to solve for the unknown variable, add $\frac{7}{8}$ on both sides of the equation.

$\frac{1}{2}x -\frac{7}{8} +\frac{7}{8}= \frac{15}{8}+\frac{7}{8}$

Simplify both sides of the equation. The denominators are like, which means we do not need to find a lowest common denominator.

$\frac{1}{2}x = \frac{15}{8}+\frac{7}{8}$

Add the numerators on the right side. The denominators will remain the same.

$\frac{1}{2}x = \frac{22}{8}$

Multiply by the reciprocal of $\frac{1}{2}$ , or , on both sides to eliminate the fraction on the left side of the equation.

$\frac{1}{2}x \times2= \frac{22}{8}\times2$

Simplify both sides of the equation.

$x=\frac{44}{8}$

This fraction can still be reduced. Expand by their common factors.

$x=\frac{44}{8} = \frac{11 \times 4}{2 \times 4} = \frac{11}{2}$

Report an Error

Example Question #28 : Two Step Equations With Fractions

Solve: $\frac{3}{4}x +\frac{3}{4}= \frac{7}{8}$

Possible Answers:

$\frac{1}{2}$

$\frac{1}{6}$

$\frac{8}{21}$

$\frac{5}{2}$

Correct answer:

$\frac{1}{6}$

Explanation:

Subtract $\frac{3}{4}$ on both sides of the equation.

$\frac{3}{4}x +\frac{3}{4}-\frac{3}{4}= \frac{7}{8}-\frac{3}{4}$

Simplify the left side of the equation.

$\frac{3}{4}x= \frac{7}{8}-\frac{3}{4}$

The numerators on the right side of the equation cannot be subtracted unless both denominators are the same. The least common denominator is . Multiply both the numerator and denominator of $\frac{3}{4}$ by two to get the common denominator.

$\frac{3}{4}x= \frac{7}{8}-\frac{3(2)}{4(2)}$

$\frac{3}{4}x= \frac{7}{8}-\frac{6}{8}$

Subtract the numerators on the right side of the equation.

$\frac{3}{4}x= \frac{1}{8}$

Multiply the reciprocal of $\frac{3}{4}$ , or $\frac{4}{3}$ , in order to isolate .

$\frac{3}{4}x \times \frac{4}{3}= \frac{1}{8}\times \frac{4}{3}$

Simplify both sides.

$x= \frac{1}{8}\times \frac{4}{3} = \frac{4}{24} = \frac{1}{6}$

Report an Error

Example Question #24 : Two Step Equations With Fractions

$8 \left(\frac{1}{2}x + 6\right) = 24$

Possible Answers:

x = -8

x = 12

x = 8

x = 6

x = -6

Correct answer:

x = -6

Explanation:

$8 \left(\frac{1}{2}x + 6\right) = 24$

Use the distributive Property first to distribute the eight to both terms within the parentheses.

$\left(8 * \frac{1}{2}x\right) + (8 * 6) = 24$

Simplify from here.

First subtract 48 from both sides.

(4x) + (48) = 24

Now divide by four to isolate and solve for x.

$\frac{4x}{4} = \frac{-24}{4}$

x = - 6

Report an Error

Example Question #31 : Two Step Equations With Fractions

Find the solution for s.

$\frac{3}{6}+\frac{2}{3}s=\frac{3}{5}$

Possible Answers:

$s=\frac{18}{15}$

$s=\frac{6}{4}$

$s=\frac{3}{20}$

$s=\frac{1}{5}$

$s=\frac{3}{5}$

Correct answer:

$s=\frac{3}{20}$

Explanation:

This is a two-step equation. The first step is as follows:

$\frac{3}{6}-\frac{3}{6}+\frac{2}{3}s=\frac{3}{5}-\frac{3}{6}$

$\frac{2}{3}s=\frac{3}{5}-\frac{3}{6} \Rightarrow\frac{2}{3}s=\frac{18}{30}-\frac{15}{30}\Rightarrow \frac{2}{3}s=\frac{3}{30}$

Now we divide both sides by 2/3 as follows:

$\frac{\frac{2}{3}s}{\frac{2}{3}}=\frac{\frac{3}{30}}{\frac{2}{3}}$

$s=\frac{\frac{3}{30}}{\frac{2}{3}}\Rightarrow s=\frac{3}{30}\cdot \frac{3}{2}$

$s= \frac{9}{60}=\frac{3}{20}$

Report an Error

Example Question #91 : Two Step Equations

$\frac{2}{3}m = 12$

Possible Answers:

m = 8

m = 18

m = 14

m = 36

$m = \frac{2}{3}$

Correct answer:

m = 18

Explanation:

To solve the equation,

$\frac{2}{3}m = 12$

use inverse operations.

Multiply both sides by ,

2m = 36

Divide both sides by ,

m = 18

Report an Error

Example Question #33 : Two Step Equations With Fractions

Simplify the following

$\frac{3}{5}x=\frac{9}{5}$

Possible Answers:

x=9

x=10

x=3

x=5

x=2

Correct answer:

x=3

Explanation:

This is a two-step problem where you need to isolate x.

The first step is to multiply everything by , which gives you:

3x=9 because the fives on both sides will cancel.

The next and last step is to divide both sides by which gives you a final answer of:

x=3

Report an Error

Example Question #31 : Two Step Equations With Fractions

$3\frac{5}{8}+4\frac{1}{2}= ?$

The answer must be a mixed number.

Possible Answers:

$11\frac{7}{8}$

$\frac{65}{8}$

$4\frac{5}{8}$

$8\frac{1}{8}$

Correct answer:

$8\frac{1}{8}$

Explanation:

The first step to adding mixed numbers is to convert them into improper fractions.

$3\frac{5}{8}=\frac{[(3\times8)+5]}{8} = \frac{29}{8}$

$4\frac{1}{2}=\frac{[(4\times2)+1]}{2}=\frac{9}{2}$

Next, find the least common multiple of 2 and 8 so that both fractions have the same denominator.

$\frac{9}{2}\times\frac{4}{4}=\frac{36}{8}$

Now that the denominators of both fractions are the same, add the fractions.

$\frac{29}{8}+\frac{36}{8}=\frac{65}{8}$

Convert the improper fraction back into a mixed number.

65 divided by 8 is 8 remainder 1, or $8\frac{1}{8}$ .

Report an Error

Example Question #31 : Two Step Equations With Fractions

$3\frac{5}{8}+4\frac{1}{2}= ?$

The answer must be a mixed number.

Possible Answers:

$11\frac{7}{8}$

$\frac{65}{8}$

$4\frac{5}{8}$

$8\frac{1}{8}$

Correct answer:

$8\frac{1}{8}$

Explanation:

The first step to adding mixed numbers is to convert them into improper fractions.

$3\frac{5}{8}=\frac{[(3\times8)+5]}{8} = \frac{29}{8}$

$4\frac{1}{2}=\frac{[(4\times2)+1]}{2}=\frac{9}{2}$

Next, find the least common multiple of 2 and 8 so that both fractions have the same denominator.

$\frac{9}{2}\times\frac{4}{4}=\frac{36}{8}$

Now that the denominators of both fractions are the same, add the fractions.

$\frac{29}{8}+\frac{36}{8}=\frac{65}{8}$

Convert the improper fraction back into a mixed number.

65 divided by 8 is 8 remainder 1, or $8\frac{1}{8}$ .

Report an Error

Example Question #1 : Two Step Equations With Decimals

Solve for :

0.33x+1.66=9.99

Possible Answers:

$25.\overline{42}$

$-25.\overline{42}$

$25.\overline{24}$

$-25.\overline{24}$

Correct answer:

$25.\overline{24}$

Explanation:

The goal is to isolate the variable to one side.

0.33x+1.66=9.99

Subtract 1.66 from both sides:

0.33x+1.66-1.66=9.99-1.66

0.33x=8.33

Divide each side by 0.33 :

$\frac{0.33x}{0.33}=\frac{8.33}{0.33}$

$x=25.\overline{24}$

Report an Error

Example Question #2 : Two Step Equations With Decimals

Solve for :

.5x+.08=1.68

Possible Answers:

3.28

3.44

3.2

Correct answer:

3.2

Explanation:

Step 1: Subtract from both sides:

.5x+.08-.08=1.68-.08

.5x+0=1.6

.5x=1.6

Step 2: Divide both sides by :

$\frac{.5x}{.5}= \frac{1.6}{.5}$

x=3.2

Report an Error

View Pre-Algebra Tutors

Owen
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Biology, General.

View Pre-Algebra Tutors

Robert
Certified Tutor

University of Pittsburgh, Bachelor of Science, Physics.

View Pre-Algebra Tutors

Kara
Certified Tutor

Syracuse University, Bachelor of Science, Exercise Science. Georgetown University, Master of Science, Physiology.

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in New York City, Physics Tutors in Atlanta, SAT Tutors in Dallas Fort Worth, GRE Tutors in Chicago, Physics Tutors in Seattle, Chemistry Tutors in Miami, SAT Tutors in San Diego, Computer Science Tutors in Miami, Spanish Tutors in Philadelphia, SSAT Tutors in Los Angeles

Popular Courses & Classes

SSAT Courses & Classes in Denver, GRE Courses & Classes in Seattle, GRE Courses & Classes in San Diego, ACT Courses & Classes in Chicago, GRE Courses & Classes in Houston, ACT Courses & Classes in Houston, MCAT Courses & Classes in New York City, Spanish Courses & Classes in Boston, SSAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Phoenix

Popular Test Prep

LSAT Test Prep in San Diego, GMAT Test Prep in Chicago, SSAT Test Prep in Philadelphia, LSAT Test Prep in Phoenix, SAT Test Prep in Boston, ISEE Test Prep in Houston, LSAT Test Prep in Seattle, ACT Test Prep in Phoenix, GMAT Test Prep in Philadelphia, SSAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Two-Step Equations

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #22 : Two Step Equations With Fractions

Example Question #28 : Two Step Equations With Fractions

Example Question #24 : Two Step Equations With Fractions

Example Question #31 : Two Step Equations With Fractions

Example Question #91 : Two Step Equations

Example Question #33 : Two Step Equations With Fractions

Example Question #31 : Two Step Equations With Fractions

Example Question #31 : Two Step Equations With Fractions

Example Question #1 : Two Step Equations With Decimals

Example Question #2 : Two Step Equations With Decimals

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: