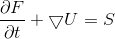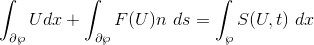Call Now to Set Up Tutoring:

(888) 888-0446

Partial Differential Equations : Partial Differential Equations

Study concepts, example questions & explanations for Partial Differential Equations

Create An Account

All Partial Differential Equations Resources

11 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Partial Differential Equations

Solve the Boundary Value Problem (BVP).

$\\y'+16y=0 \\y(0)=-4 \\\\y\left(\frac{\pi}{2} \right )=5$

Possible Answers:

$y(x)=4\cos(4x)-5\sin(4x)$

$y(x)=-5\cos(4x)+4\sin(4x)$

$y(x)=-4\cos(4x)+5\sin(4x)$

$y(x)=5\cos(4x)-4\sin(4x)$

$y(x)=-4\cos(16x)+5\sin(16x)$

Correct answer:

$y(x)=-4\cos(4x)+5\sin(4x)$

Explanation:

To solve this Boundary Value Problem (BVP) recall that the general solution for this type of derivative is,

$\\y'+ay=0 \\y(x)=c_1\cos(\sqrt{a}x)+c_2\sin(\sqrt{a}x)$

Therefore, the equation becomes

$y(x)=c_1\cos(4x)+c_2\sin(4x)$

From here, apply the boundary conditions to solve for the constants c_1 and c_2

$\\-4=y(0)=c_1 \\\\5=y\left(\frac{\pi}{2} \right )=c_2$

Thus resulting in the solution,

$y(x)=-4\cos(4x)+5\sin(4x)$

Report an Error

Example Question #2 : Partial Differential Equations

Solve the Boundary Value Problem (BVP).

$\\y'+9y=0 \\y(0)=-7 \\\\y\left(\frac{\pi}{2} \right )=2$

Possible Answers:

$y(x)=-2\cos(3x)+7\sin(3x)$

$y(x)=-3\cos(7x)+3\sin(2x)$

$y(x)=-7\cos(3x)-2\sin(3x)$

$y(x)=7\cos(3x)+2\sin(3x)$

$y(x)=-7\cos(3x)+2\sin(3x)$

Correct answer:

$y(x)=-7\cos(3x)+2\sin(3x)$

Explanation:

To solve this Boundary Value Problem (BVP) recall that the general solution for this type of derivative is,

$\\y'+ay=0 \\y(x)=c_1\cos(\sqrt{a}x)+c_2\sin(\sqrt{a}x)$

Therefore, the equation becomes

$y(x)=c_1\cos(3x)+c_2\sin(3x)$

From here, apply the boundary conditions to solve for the constants c_1 and c_2

$\\-7=y(0)=c_1 \\\\2=y\left(\frac{\pi}{2} \right )=c_2$

Thus resulting in the solution,

$y(x)=-7\cos(3x)+2\sin(3x)$

Report an Error

Example Question #3 : Partial Differential Equations

Determine if the statement is true or false:

The wave equation has at most one solution.

Possible Answers:

True

False

Correct answer:

True

Explanation:

This statement is true by the Uniqueness Theorem.

$\\u_{tt}=c^2u_{xx}, 0<x<1, t>0 \\\text{Initial Conditions: }u(x,0)=f(x), u_t(x,0)=g(x), 0\leq x\leq l \\\text{Boundary Conditions: }u(0,t)=0, u(l,t)=0, t\geq 0$

u(x,t) is twice differential equation in terms of and .

Now, consider the energy integral

$E(t)=\frac{1}{2}\int_0^l(c^2u^2_x+u^2_t)\ dx$

After performing integration by parts results in the following,

$\int_0^lc^2u_xu_{xt}\ dx=[c^2u_xu_t]_0^l-\int_0^lc^2u_tu_{xx}\ dx$

From here, the initial conditions and boundary conditions are applied.

$\\\frac{dE}{dt}=\int_0^l u_t(u_{tt}-c^2u_{xx})\ dx \\\\\frac{dE}{dt}=0 \\\\E(t)=C$

Therefore,

u_1(x,t)=u_2(x,t)=u(x,t)

which proves the wave equations has only one solution and thus is unique.

Report an Error

Example Question #1 : Derivatives From Conservation Laws

What is the conservation law written as a partial differential equation?

Possible Answers:

$\int_{\partial \wp } U dx+\int_{\partial \wp} F(U)n\ ds=\int_\wp S(U,t)\ dx$

$\int_{\partial \wp } U dx+\int_{\partial \wp} F(U)n\ ds$

$\frac{\partial U}{\partial t}+\bigtriangledown S=F$

$\frac{\partial F}{\partial t}+\bigtriangledown U=S$

$\frac{\partial U}{\partial t}+\bigtriangledown F=S$

Correct answer:

$\frac{\partial U}{\partial t}+\bigtriangledown F=S$

Explanation:

The conservation law written as a partial differential equation is found by applying the divergence theorem to the conservation equation.

The conservation equation is,

$\frac{d}{dt}\int_\wp U\ dx +\int_{\partial \wp} F(U)n\ ds=\int_\wp S(U,t)\ dx$

Now, recall the divergence theorem which states,

$\int_{\partial \wp}Fn\ ds=\int_{\wp}\bigtriangledown F\ dx$

Thus, by substituting

$\int_{\partial \wp} Fn\ ds$ for $\int_{\partial \wp} F(U)n\ ds$ results in,

$\frac{d}{dt}\int_\wp U\ dx+\int_{\partial \wp}Fn\ ds=\int_\wp S\ dx$

From here, rewriting this equation to bring the derivative inside the integral along with substituting

$\int_{\partial \wp} Fn\ ds=\int_\wp \bigtriangledown F\ ds$ ,

and performing some algebraic operations results in,

$\int_\wp \left(\frac{\partial U}{\partial t}+\bigtriangledown F-S \right )dx=0$

After integrating over the domain $\wp$ the partial differential equation that is found is,

$\frac{\partial U}{\partial t}+\bigtriangledown F=S$

Report an Error

Example Question #2 : Derivatives From Conservation Laws

What is the order of the following partial differential equation.

$u_{xx}+2u_{xy}+\frac{7}{5}u_{yy}=10y$

Possible Answers:

First Order

Third Order

Second Order

Quasi Linear

Linear

Correct answer:

Second Order

Explanation:

Just like with ordinary differential equations, partial differential equations can be characterized by their order.

The order of an equation is defined by the highest ordered partial derivatives in the equations.

Looking at the equation in question,

$u_{xx}+2u_{xy}+\frac{7}{5}u_{yy}=10y$

The partial derivatives are:

$\\u_{xx} \\u_{xy} \\u_{yy}$

Notice that each partial derivative contains two variables, thus this equation is a second order partial differential equation.

Report an Error

Example Question #2 : Partial Differential Equations

What is the order of the following partial differential equation.

$u_{xyz}+u_{xy}+\frac{10}{3}=10y$

Possible Answers:

Second Order

Linear

Third Order

First Order

Quasi Linear

Correct answer:

Third Order

Explanation:

Just like with ordinary differential equations, partial differential equations can be characterized by their order.

The order of an equation is defined by the highest ordered partial derivatives in the equations.

Looking at the equation in question,

$u_{xyz}+u_{xy}+\frac{10}{3}=10y$

The partial derivatives are:

$\\u_{xyz} \\u_{xy}$

Notice that one of them partial derivative contains three variables, thus this equation is a third order partial differential equation.

Report an Error

Example Question #6 : Partial Differential Equations

Which of the following describes the physical phenomena that is the biharmonic wave equation?

Possible Answers:

$u_{tt}+c^2\bigtriangledown^4u=0$

$u_{xx}+u_{yy}+u_{zz}=0$

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$

$\bigtriangledown^2u=f(x,y,z)$

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$

Correct answer:

$u_{tt}+c^2\bigtriangledown^4u=0$

Explanation:

When dealing with partial differential equations, there are phenomenons in the physical world that have specific equations related to them in the mathematical world.

Looking at the possible answer selections below, identify the physical phenomena each represents.

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$ is known as the heat equation.

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$ is known as the wave equation.

$u_{xx}+u_{yy}+u_{zz}=0$ is known as the Laplace equation.

$\bigtriangledown^2u=f(x,y,z)$ is known as the Poisson equation.

$u_{tt}+c^2\bigtriangledown^4u=0$ is known as the biharmonic wave equation.

Therefore, the correct answer for the biharmonic wave equation is

$u_{tt}+c^2\bigtriangledown^4u=0$

Report an Error

Example Question #3 : Partial Differential Equations

What is the order of the following partial differential equation.

$u_{xyz}+u_{xy}=e^y$

Possible Answers:

First Order

Non-homogenous

Third Order

Homogeneous

Second Order

Correct answer:

Third Order

Explanation:

Just like with ordinary differential equations, partial differential equations can be characterized by their order.

The order of an equation is defined by the highest ordered partial derivatives in the equations.

Looking at the equation in question,

$u_{xyz}+u_{xy}=e^y$

The partial derivatives are:

$\\u_{xyz} \\u_{xy}$

Notice that one of them partial derivative contains three variables, thus this equation is a third order partial differential equation.

Report an Error

Example Question #1 : Linear & Quasi Linear Pd Es

Determine if the statement is true or false:

If the -axis is the axis of symmetry and a surface is revolving around it and is an arbitrary function, then the partial differential equation associated with that said surface, satisfies the equation:

z=f(x^2+y^2)

Possible Answers:

True

False

Correct answer:

True

Explanation:

To determine the truth of this statement, assume the following.

is some function

u=x^2+y^2

From here, differential with respect to and .

z=f(x^2+y^2)

$\\\frac{dz}{dx}=2x\cdot f'(u) \\\\\frac{dz}{dy}=2y\cdot f'(u)$

Next eliminate f'(u) as it is an arbitrary function.

This leads to the result,

$y\cdot \frac{dz}{dx}-x\cdot \frac{dy}{dz}=0$

Therefore, the statement,

z=f(x^2+y^2)

is true.

Report an Error

Example Question #2 : Partial Differential Equations

Which of the following describes the physical phenomena that is the wave equation?

Possible Answers:

$\bigtriangledown^2u=f(x,y,z)$

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$

$u_{xx}+u_{yy}+u_{zz}=0$

$u_{tt}+c^2\bigtriangledown^4u=0$

Correct answer:

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$

Explanation:

When dealing with partial differential equations, there are phenomenons in the physical world that have specific equations related to them in the mathematical world.

Looking at the possible answer selections below, identify the physical phenomena each represents.

$u_t-k(u_{xx}+u_{yy}+u_{zz})=0$ is known as the heat equation.

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$ is known as the wave equation.

$u_{xx}+u_{yy}+u_{zz}=0$ is known as the Laplace equation.

$\bigtriangledown^2u=f(x,y,z)$ is known as the Poisson equation.

$u_{tt}+c^2\bigtriangledown^4u=0$ is known as the biharmonic wave equation.

Therefore, the correct answer for the wave equation is

$u_{tt}-c^2(u_{xx}+u_{yy}+u_{zz})=0$

Report an Error

View Tutors

Jason
Certified Tutor

The University of Tennessee-Martin, Bachelor of Science, Social Studies Teacher Education. Union University, Masters in Busin...

View Tutors

Muhammad
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Mechanical Engineering.

View Tutors

Alesia
Certified Tutor

University of Phoenix-Houston Campus, Bachelor of Science, Information Technology.

All Partial Differential Equations Resources

11 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Chicago, SSAT Tutors in Los Angeles, Algebra Tutors in Philadelphia, Spanish Tutors in Atlanta, ISEE Tutors in New York City, ISEE Tutors in Phoenix, Reading Tutors in Los Angeles, Math Tutors in Atlanta, GRE Tutors in Seattle, English Tutors in San Francisco-Bay Area

Popular Courses & Classes

SSAT Courses & Classes in Washington DC, LSAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Los Angeles, MCAT Courses & Classes in San Diego, MCAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Seattle, GMAT Courses & Classes in Boston, LSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Houston

Popular Test Prep

GRE Test Prep in Miami, ISEE Test Prep in Atlanta, GRE Test Prep in Atlanta, GMAT Test Prep in Chicago, GRE Test Prep in Boston, SSAT Test Prep in Washington DC, MCAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Seattle, ISEE Test Prep in Seattle, ISEE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Partial Differential Equations : Partial Differential Equations

Study concepts, example questions & explanations for Partial Differential Equations

All Partial Differential Equations Resources

Example Questions

Example Question #1 : Partial Differential Equations

Example Question #2 : Partial Differential Equations

Example Question #3 : Partial Differential Equations

Example Question #1 : Derivatives From Conservation Laws

Example Question #2 : Derivatives From Conservation Laws

Example Question #2 : Partial Differential Equations

Example Question #6 : Partial Differential Equations

Example Question #3 : Partial Differential Equations

Example Question #1 : Linear & Quasi Linear Pd Es

Example Question #2 : Partial Differential Equations

All Partial Differential Equations Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: