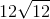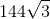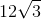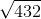Call Now to Set Up Tutoring:

(888) 888-0446

New SAT Math - Calculator : New SAT Math - Calculator

Study concepts, example questions & explanations for New SAT Math - Calculator

Create An Account

All New SAT Math - Calculator Resources

2 Diagnostic Tests 27 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Find An Angle Of A Line

If $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ , $\overline{BE}\perp \overleftrightarrow{GC}$ , and $m\angle HGC=58^\circ$ , what is the measure, in degrees, of $\angle ABE$ ?

Alternate interior angles

Possible Answers:

122

148

Correct answer:

148

Explanation:

The question states that $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ . The alternate interior angle theorem states that if two parallel lines are cut by a transversal, then pairs of alternate interior angles are congruent; therefore, we know the following measure:

$m\angle GCA = 58^\circ$

The sum of angles of a triangle is equal to 180 degrees. The question states that $\overline{BE}\perp \overleftrightarrow{GC}$ ; therefore we know the following measure:

$m \angle BEC = 90^\circ$

Use this information to solve for the missing angle: $\angle EBC$

$180^\circ=m\angle EBC+58^\circ+90^\circ$

$m\angle EBC=32^\circ$

The degree measure of a straight line is 180 degrees; therefore, we can write the following equation:

$180^\circ=m\angle ABE+32^\circ$

$m\angle ABE=148^\circ$

The measure of $\angle ABE$ is 148 degrees.

Report an Error

Example Question #1 : How To Find An Angle Of A Line

Lines A and B in the diagram below are parallel. The triangle at the bottom of the figure is an isosceles triangle.

Act2

What is the degree measure of angle ?

Possible Answers:

Correct answer:

Explanation:

Since A and B are parallel, and the triangle is isosceles, we can use the supplementary rule for the two angles, and 2x+30 which will sum up to 180 . Setting up an algebraic equation for this, we get 4x+2x+30=180 . Solving for , we get x=25 . With this, we can get either 2(25)+30=80 (for the smaller angle) or 4(25)=100 (for the larger angle - must then use supplementary rule again for inner smaller angle). Either way, we find that the inner angles at the top are 80 degrees each. Since the sum of the angles within a triangle must equal 180, we can set up the equation as 80+80+y=180

y=20 degrees.

Report an Error

Example Question #1 : How To Simplify Square Roots

Which of the following is equal to $\sqrt{75}$ ?

Possible Answers:

$3\sqrt{5}$

$7.5\sqrt{10}$

$5\sqrt{3}$

Correct answer:

$5\sqrt{3}$

Explanation:

√75 can be broken down to √25 * √3. Which simplifies to 5√3.

Report an Error

Example Question #1 : How To Simplify Square Roots

Simplify $\sqrt{a^{3}b^{4}c^{5}}$ .

Possible Answers:

$a^{2}b^{2}c\sqrt{ab}$

$a^{2}bc^{2}\sqrt{ac}$

$ab^{2}c^{2}\sqrt{ac}$

$a^{2}b^{2}c^{2}\sqrt{bc}$

$a^{2}bc\sqrt{bc}$

Correct answer:

$ab^{2}c^{2}\sqrt{ac}$

Explanation:

Rewrite what is under the radical in terms of perfect squares:

$x^{2}=x\cdot x$

$x^{4}=x^{2}\cdot x^{2}$

$x^{6}=x^{3}\cdot x^{3}$

Therefore, $\sqrt{a^{3}b^{4}c^{5}}= \sqrt{a^{2}a^{1}b^{4}c^{4}c^{1}}=ab^{2}c^{2}\sqrt{ac}$ .

Report an Error

Example Question #1 : How To Simplify Square Roots

What is $\sqrt{50}$ ?

Possible Answers:

$10\sqrt{2}$

$5\sqrt{2}$

$2\sqrt{5}$

Correct answer:

$5\sqrt{2}$

Explanation:

We know that 25 is a factor of 50. The square root of 25 is 5. That leaves $\sqrt{2}$ which can not be simplified further.

Report an Error

Example Question #1 : How To Simplify Square Roots

Which of the following is equivalent to $\frac{x + \sqrt{3}}{3x + \sqrt{2}}$ ?

Possible Answers:

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

$\frac{4x + \sqrt{5}}{3x + 2}$

$\frac{3x^{2} - \sqrt{6}}{9x^{2} + 2}$

$\frac{3x^{2} + \sqrt{6}}{3x - 2}$

$\frac{3x^{2} + 3x\sqrt{2} + x\sqrt{3} +\sqrt{6}}{9x^{2} - 2}$

Correct answer:

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Explanation:

Multiply by the conjugate and the use the formula for the difference of two squares:

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}$

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}\cdot \frac{3x - \sqrt{2}}{3x - \sqrt{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{(3x)^{2} - (\sqrt{2})^{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Report an Error

Example Question #1 : How To Simplify Square Roots

Which of the following is the most simplified form of:

$\sqrt{468}$

Possible Answers:

$4\sqrt{29}$

$\sqrt{468}$

$17\sqrt{2}$

$6\sqrt{13}$

$2\sqrt{117}$

Correct answer:

$6\sqrt{13}$

Explanation:

First find all of the prime factors of 468

$468=6\ast78=6\ast6\ast13=2\ast3\ast2\ast3\ast13$

So $\sqrt{468}=\sqrt{2\ast2\ast3\ast3\ast13}=2\ast3\sqrt{13}=6\sqrt{13}$

Report an Error

Example Question #801 : New Sat

What is $\sqrt{432}$ equal to?

Possible Answers:

$6\sqrt{4}$

$12\sqrt{3}$

$144\sqrt{3}$

$12\sqrt{12}$

$6\sqrt{3}$

Correct answer:

$12\sqrt{3}$

Explanation:

$\sqrt{432}$

1. We know that 432=(144)(3) , which we can separate under the square root:

$\sqrt{144\cdot 3}$

2. 144 can be taken out since it is a perfect square: $12\cdot12=144$ . This leaves us with:

$12\sqrt{3}$

This cannot be simplified any further.

Report an Error

Example Question #1 : How To Simplify Square Roots

Which of the following is equal to $\small \sqrt{420}$ ?

Possible Answers:

$\small 2\sqrt{105}$

$\small 6\sqrt{35}$

$\small 28\sqrt{5}$

$\small \small 3\sqrt{70}$

$\small 4\sqrt{35}$

Correct answer:

$\small 2\sqrt{105}$

Explanation:

When simplifying square roots, begin by prime factoring the number in question. For $\small 420$ , this is:

$\small 420 = 2*2*3*5*7$

Now, for each pair of numbers, you can remove that number from the square root. Thus, you can say:

$\small \small \sqrt{420}=2\sqrt{105}$

Another way to think of this is to rewrite $\small \small \sqrt{420}$ as $\small \sqrt{4}*\sqrt{105}$ . This can be simplified in the same manner.

Report an Error

Example Question #8 : Exponents And Roots

Which of the following is equivalent to $\small \sqrt{700700}$ ?

Possible Answers:

$\small 770\sqrt{13}$

$\small 70\sqrt{143}$

$\small 100\sqrt{77}$

$\small 90\sqrt{11}$

$\small 121\sqrt{7}$

Correct answer:

$\small 70\sqrt{143}$

Explanation:

When simplifying square roots, begin by prime factoring the number in question. This is a bit harder for $\small 700700$ . Start by dividing out $\small 100$ :

$\small 700700 = 7007 * 100$

Now, $\small 7007$ is divisible by , so:

$\small \small 700700 =1001 * 7 * 2*2*5*5$

$\small 1001$ is a little bit harder, but it is also divisible by $\small 7$ , so:

$\small 700700 =143*7 * 7 * 2*2*5*5$

With some careful testing, you will see that $\small 143 = 11 * 13$

Thus, we can say:

$\small \small 700700 = 2*2*5*5*7 * 7*11*13$

Now, for each pair of numbers, you can remove that number from the square root. Thus, you can say:

$\small \small \sqrt{700700} = 2*5*7*\sqrt{143}=70\sqrt{143}$

Another way to think of this is to rewrite $\small \small \small \sqrt{700700}$ as $\small \sqrt{4} * \sqrt{25} * \sqrt{49} * \sqrt{143}$ . This can be simplified in the same manner.

Report an Error

View Tutors

Julien
Certified Tutor

University of Prince Edward Island, Bachelor, English.

View Tutors

Fiona
Certified Tutor

University of Toronto, Bachelor in Arts, Religious Studies. University of Toronto, Bachelor of Science, Mathematics.

View Tutors

Ayotunde
Certified Tutor

Johns Hopkins University, Bachelor of Science, Mechanical Engineering.

All New SAT Math - Calculator Resources

2 Diagnostic Tests 27 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in San Diego, Physics Tutors in San Francisco-Bay Area, GMAT Tutors in Philadelphia, SAT Tutors in San Diego, GRE Tutors in Houston, Math Tutors in Atlanta, ACT Tutors in Denver, Biology Tutors in Miami, SSAT Tutors in Atlanta, GMAT Tutors in Houston

Popular Courses & Classes

MCAT Courses & Classes in Seattle, GMAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Denver, Spanish Courses & Classes in Philadelphia, GRE Courses & Classes in San Diego, GRE Courses & Classes in Philadelphia, Spanish Courses & Classes in Miami, Spanish Courses & Classes in New York City, MCAT Courses & Classes in Denver, ISEE Courses & Classes in Denver

Popular Test Prep

SSAT Test Prep in Phoenix, ISEE Test Prep in Miami, ISEE Test Prep in Atlanta, MCAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Philadelphia, GRE Test Prep in Chicago, ISEE Test Prep in New York City, SSAT Test Prep in Boston, GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

New SAT Math - Calculator : New SAT Math - Calculator

Study concepts, example questions & explanations for New SAT Math - Calculator

All New SAT Math - Calculator Resources

Example Questions

Example Question #11 : How To Find An Angle Of A Line

Example Question #1 : How To Find An Angle Of A Line

Example Question #1 : How To Simplify Square Roots

Example Question #1 : How To Simplify Square Roots

Example Question #1 : How To Simplify Square Roots

Example Question #1 : How To Simplify Square Roots

Example Question #1 : How To Simplify Square Roots

Example Question #801 : New Sat

Example Question #1 : How To Simplify Square Roots

Example Question #8 : Exponents And Roots

All New SAT Math - Calculator Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: