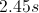Call Now to Set Up Tutoring:

(888) 888-0446

MCAT Physical : Motion in Two Dimensions

Study concepts, example questions & explanations for MCAT Physical

Create An Account

All MCAT Physical Resources

8 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #51 : Translational Motion

A 2kg lead ball is loaded into a spring cannon and the cannon is set at a 45º angle on a platform. The spring has a spring constant of 100N/m and the ball and spring system is compressed by 1m before launch. While the ball is in flight air resistance can be neglected, and the ball finishes its flight by landing at a cushion placed some distance away from the cannon.

What are the horizontal and vertical velocities of the ball right before it hits the ground?

Possible Answers:

v_fx = 7.1m/s

v_fy = 7.1m/s

v_fx = 4.15m/s

v_fy = 9.42m/s

v_fy = 5.25m/s

v_fx = 8.51m/s

v_fx = 0m/s

v_fy = 0m/s

Correct answer:

v_fx = 7.1m/s

v_fy = 7.1m/s

Explanation:

The final and initial velocities are the same if air resistance can be neglected and the start and end positions are at the same height. Kinetic and potential energy must be conserved if there are no frictional forces acting against motion, so the final and initial velocities must be the same.

v_fx = (10 m/s)(cos(45^o)) = 7.1m/s

v_fy = (10 m/s)(sin(45^o)) = 7.1m/s

Report an Error

Example Question #12 : Motion In Two Dimensions

A cannon fires a cannon ball at an angle of 60^o relative to the ground. The cannon ball comes out at an initial velocity of $\small 120 \frac{m}{s}$ . Assume there is no air resistance.

What is the cannon ball's maximum height off of the ground?

Possible Answers:

540m

360 m

720 m

180 m

Correct answer:

540m

Explanation:

In order to find the maximum height of the cannonball from the ground, we can use the equation $\small v_{0}sin(\theta) = \sqrt{2gh}$ , with g being the acceleration due to gravity, and h being the height.

$\small 120sin(60^{\circ}) = \sqrt{2(10)(h)}$

$\small h = 540 m$

Report an Error

Example Question #281 : Mcat Physical Sciences

A cannon fires a cannon ball at an angle of 60^o relative to the ground. The cannon ball comes out at an initial velocity of $\small 120 \frac{m}{s}$ . Assume there is no air resistance.

How long will the cannon ball stay in the air?

Possible Answers:

10.4 s

20.8 s

24.0 s

12.2s

Correct answer:

20.8 s

Explanation:

In order to solve for the amount of time, we need to know the vertical initial velocity of the cannonball. This is given by the equation $\small v_{0}sin(60^{\circ})$ . Using the initial velocity of $\small \small 120\frac{m}{s},$ we determine that the vertical initial velocity is $\small 104\frac{m}{s}.$

Knowing this, we can solve the amount of time it will take for the cannon ball to reach its maximum peak, with a velocity of $\small 0\frac{m}{s}$ using the equation $\small v = v_{0} + at$

$\small 0 = 104\frac{m}{s} + (-10\frac{m}{s^{2}})(t)$

$\small t = 10.4 s$

This is the amount of time it takes for the ball to reach its peak, not the total time it is in the air. Since the ball must drop from the maximum height, we double the time and arrive at the correct answer of 20.8s.

Report an Error

Example Question #282 : Mcat Physical Sciences

A cannon fires a cannon ball at an angle of 60^o relative to the ground. The cannon ball comes out at an initial velocity of $\small 120 \frac{m}{s}$ . Assume there is no air resistance.

Which of the following statements is true?

Possible Answers:

The vertical velocity of the cannon ball changes during its flight

The horizontal velocity of the ball changes during its flight

None of these vectors change during the ball's flight

The acceleration of the ball changes during its flight

Correct answer:

The vertical velocity of the cannon ball changes during its flight

Explanation:

The only acceleration on the cannon ball is done by gravity, which is constant throughout the ball's flight. Since there is no air resistance, the horizontal velocity of the ball is also constant, however, the vertical velocity of the ball is not constant, because the velocity of the ball changes throughout its flight.

It is $\small 103.9\frac{m}{s}$ at the beginning ( $\small v_{0}sin(60^{\circ})$ )and is $\small 0\frac{m}{s}$ at the maximum height of the cannon ball.

Report an Error

Example Question #52 : Translational Motion

An object is shot from the ground at 75m/s at an angle of 45⁰ above the horizontal. How high does the object get before beginning its descent?

Possible Answers:

140m

280m

420m

70m

Correct answer:

140m

Explanation:

The velocity must be broken down into x (horizontal) and y (vertical) components. We can use the y component to find how high the object gets. To find vertical velocity, v_y, use $v_y = v_o sin\theta$ .

$v_y = (75 \frac{m}{s})sin 45^o = 53 \frac{m}{s}$

Next we find how long it takes to reach the top of its trajectory using v_f = v_o +at .

$0 \frac{m}{s} = 53 \frac{m}{s} + (-10 \frac{m}{s^2})t$

t = 5.3s

Finally, find how high the object goes with $d = v_ot +\frac{1}{2}at^{2}$ .

$d = (53\frac{m}{s})5.3s + \frac{1}{2}(-10\frac{m}{s^2})(5.3s)^{2} = 140 m$

Report an Error

Example Question #1 : Motion In Two Dimensions

An object is shot from the ground at 125m/s at an angle of 30^o above the horizontal. How far away does the object land?

Possible Answers:

62.5m

675m

250m

1350m

Correct answer:

1350m

Explanation:

First, find the horizontal (x) and vertical (y) components of the velocity

$v_x = v_o cos\theta$

$v_x = (125 \frac{m}{s}) cos(30^o) = 108\frac{m}{s}$

$v_y = v_o sin\theta$

$v_y = (125\frac{m}{s})sin(30^o) = 62.5\frac{m}{s}$

Next, find how long the object is in the air by calculating the time it takes it to reach the top of its path, and doubling that number.

v_f = v_o + at

$0 \frac{m}{s} = 62.5 \frac{m}{s} + (-10 \frac{m}{s^2})t$

t = 6.25s

Total time in the air is therefore 12.5s (twice this value).

Finally, find distance traveled my multiplying horizontal velocity and time.

d_x = v_x(t)

$d_x = 108 \frac{m}{s} (12.5s) = 1,350 m$

Report an Error

Example Question #2 : Motion In Two Dimensions

A 2kg box is at the top of a frictionless ramp at an angle of 60^o. The top of the ramp is 30m above the ground. The box is sitting still while at the top of the ramp, and is then released.

What is the velocity of the box just before it hits the ground?

Possible Answers:

$\small 0\frac{m}{s}.$

$\small 22.8\frac{m}{s}.$

$\small 37.2\frac{m}{s}.$

$\small 32.2\frac{m}{s}.$

Correct answer:

$\small 32.2\frac{m}{s}.$

Explanation:

We can start this problem by determining how much time it takes the box the reach the ground. Since the vertical distance is 30m and we know the angle of the ramp.

$\frac{1}{2}=\frac{30m}{x}\rightarrow x=60m$

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity, using the equation $\small gsin\Theta$ .

$gsin\Theta=(10)sin(60)=8.66\frac{m}{s^2}$

We can plug these values into the following distance equation and solve for time.

$\small x = x_{0} - \frac{1}{2}(gsin\Theta )t^{2}$

$\small 0 = 60 - \frac{1}{2}(8.66)t^{2}$

$\small \small t = 3.72 s$

Now that we know the acceleration on the box and the time of travel, we can use the equation $\small v = v_{0} + at$ to solve for the velocity.

$\small v = 0 + (8.66\frac{m}{s^{2}})(3.72 s) = 32.2 \frac{m}{s}$

Report an Error

Example Question #3 : Motion In Two Dimensions

A 2kg box is at the top of a frictionless ramp at an angle of 60^o . The top of the ramp is 30m above the ground. The box is sitting still while at the top of the ramp, and is then released.

When the box is released, how long will it take the box to reach the ground?

Possible Answers:

3.46s

4.21s

2.63s

2.45s

3.72s

Correct answer:

3.72s

Explanation:

We can start this problem by determining how far the box will travel on the ramp before hitting the ground. Since the vertical distance is 30m and we know the angle of the ramp, we can determine the length of the hypotenuse using the equation $\small cos(60^{\circ}) = \frac{30}{x}$ .

$\frac{1}{2}=\frac{30m}{x}\rightarrow x=60m$

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity. Because the box is on a sloped surface, the box will not experience the full acceleration of gravity, but will instead be accelerated at a value of $\small gsin\Theta$ . Since the angle is 60^o, the acceleration on the box is $\small 8.66 \frac{m}{s^{2}}.$

$gsin\Theta=(10)sin(60)=8.66\frac{m}{s^2}$

Finally, we can plug these values into the following distance equation and solve for time.

$\small x = x_{0} - \frac{1}{2}(gsin\Theta )t^{2}$

$\small 0 = 60 - \frac{1}{2}(8.66)t^{2}$

$\small \small t = 3.72 s$

Report an Error

Example Question #12 : Motion In Two Dimensions

A cannon fires a cannon ball at an angle of 60^o relative to the ground. The cannon ball comes out at an initial velocity of $\small 120 \frac{m}{s}$ . Assume there is no air resistance.

How far will the ball be from the cannon once it hits the ground?

Possible Answers:

1250 m

1730m

750 m

2160 m

2500 m

Correct answer:

1250 m

Explanation:

We must first determine the amount of time that the ball is in the air, then use the horizontal velocity to solve for the distance travelled.

Knowing this, we can solve the amount of time it will take for the cannon ball to reach its maximum peak, with a velocity of $\small 0\frac{m}{s}$ using the equation $\small v = v_{0} + at$

$\small 0 = 104\frac{m}{s} + (-10\frac{m}{s^{2}})(t)$

$\small t = 10.4 s$

This is the amount of time it takes for the ball to reach its peak, not the total time it is in the air. Since the ball must drop from the maximum height, we double the time and find that total flight time is 20.8s.

The next step is determining the horizontal initial velocity from the cannon. This is determined using the equation below.

$\small v_{0}cos(60^{\circ}) = 120cos(60^{\circ}) = 60\frac{m}{s.}$

Since we assume that there is no air resistance, we can conclude that the horizontal velocity of the cannonball will remain constant throughout its flight. As a result, the total displacement equation is simplified to the following: $\small x = x_{0} + v_{0}t$ .

$\small x = 0 + (60\frac{m}{s})(20.8 s)$

$\small x = 1250 m$

Report an Error

Example Question #12 : Motion In Two Dimensions

How high does the ball fly?

Possible Answers:

8.50m

4.91m

2.57m

5.69m

Correct answer:

2.57m

Explanation:

First, solve for the initial vertical velocity of the ball.

v_y = (10m/s)(sin(45^o)) = 7.1m/s

Think back to the 3 main kinematics equations we know:

v_f²= v_i² + 2aΔx

v_f = v_i + at

Δx = v_it + ½at²

We need to choose an equation that allows us to solve for the vertical height of the ball, given that we know the initial vertical velocity, final vertical velocity (zero), and the acceleration due to gravity (-9.8m/s²).

v_f² = v_i² + 2aΔy

Δy = (v_f² - v_i²)/2a

$\Delta y=\frac{(0\frac{m}{s})^2-(7.1\frac{m}{s})^2}{2(-9.8\frac{m}{s^2})}=2.57m$

Report an Error

View MCAT Chemical and Physical Foundations of Biological Systems Tutors

Shrikar
Certified Tutor

University of South Florida-Main Campus, Bachelor of Science, Biomedical Sciences.

View MCAT Chemical and Physical Foundations of Biological Systems Tutors

Frank
Certified Tutor

Metropolitan State University of Denver, Bachelor of Science, Biochemistry. Kirksville College of Osteopathic Medicine, Non D...

View MCAT Chemical and Physical Foundations of Biological Systems Tutors

Christy
Certified Tutor

Northern Michigan University, Bachelor in Arts, Graphic Design. Northern Michigan University, Bachelor of Science, Premedicine.

All MCAT Physical Resources

8 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in New York City, English Tutors in San Francisco-Bay Area, GMAT Tutors in Phoenix, Chemistry Tutors in Houston, Math Tutors in Dallas Fort Worth, Physics Tutors in Phoenix, Computer Science Tutors in New York City, Physics Tutors in Miami, Math Tutors in San Francisco-Bay Area, ACT Tutors in Chicago

Popular Courses & Classes

ACT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Seattle, ACT Courses & Classes in Philadelphia, SAT Courses & Classes in San Diego, LSAT Courses & Classes in Phoenix, GMAT Courses & Classes in Phoenix, LSAT Courses & Classes in Boston, SSAT Courses & Classes in New York City, GMAT Courses & Classes in Washington DC, SSAT Courses & Classes in Denver

Popular Test Prep

MCAT Test Prep in San Diego, ISEE Test Prep in Chicago, SAT Test Prep in Boston, GRE Test Prep in San Francisco-Bay Area, ACT Test Prep in Washington DC, SAT Test Prep in San Diego, ISEE Test Prep in Seattle, GRE Test Prep in Dallas Fort Worth, SSAT Test Prep in Washington DC, MCAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

MCAT Physical : Motion in Two Dimensions

Study concepts, example questions & explanations for MCAT Physical

All MCAT Physical Resources

Example Questions

Example Question #51 : Translational Motion

Example Question #12 : Motion In Two Dimensions

Example Question #281 : Mcat Physical Sciences

Example Question #282 : Mcat Physical Sciences

Example Question #52 : Translational Motion

Example Question #1 : Motion In Two Dimensions

Example Question #2 : Motion In Two Dimensions

Example Question #3 : Motion In Two Dimensions

Example Question #12 : Motion In Two Dimensions

Example Question #12 : Motion In Two Dimensions

All MCAT Physical Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: