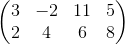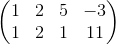Linear Algebra : Linear Equations
Study concepts, example questions & explanations for Linear Algebra
All Linear Algebra Resources
Example Questions
Example Question #61 : Reduced Row Echelon Form And Row Operations
Note that the entries in the bottom row are missing.
How many possible ways can the entries in the bottom row be filled in so that 
Three
None
Two
Infinitely many
One
Two
A matrix is in reduced row-echelon form if it meets four conditions.
1) Any rows comprising all zeroes must be below all nonzero rows.
2) All leading nonzero entries must be 1's.
3) All other entries in the same column as a leading 1 are zeroes.
4) Each leading 1 is located to the right of the one above it.
None of these four conditions have been violated, at least not yet.
First, note that there are two known leading 1's. In order for the matrix to continue to meet Condition 3, it is necessary for the first two entries in the bottom row to be zeroes.
If the third entry is nonzero, then it must be 1, since it would be a leading nonzero entry. But the third entry cannot be a leading 1, since the other entries in Column 3 are nonzero - a violation of Condition 3 would be created. This entry must be a zero.
If the last entry is a 0, then no conditions are violated; the only zero row is on the bottom, and the other conditions still hold:
If the last entry is nonzero, then it must be 1, since it would be a leading nonzero entry.No conditions are violated, since the other entries in the column are zeroes.
Therefore, the bottom row can be filled exactly two ways.
Example Question #62 : Reduced Row Echelon Form And Row Operations
Note that the top row is missing. How many ways can the top row be completed in order to form a matrix in reduced row-echelon form?
Three
Two
None
Infinitely many
One
Infinitely many
A matrix is in reduced row-echelon form if it satisfies four conditions:
1) All zero rows must be below all nonzero rows.
2) Any leading nonzero element in a nonzero row must be 1.
3) Each leading 1 must be to the right of the one above it.
4) The other elements in the same column of any leading 1 must be zeroes.
The second row has nonzero elements, so the first row cannot be all zeroes; this would violate Condition 1. There must be at least one nonzero element in the top row. The first row must have a leading 1, by Condition 2. The first nonzero element in the second row is in the second column, as seen below; the leading 1 in the first row must be in the first column,
Since leading 1's are located in the second and fourth columns, by Condition 4, the second and fourth elements in the top row must be zeroes.
However, there are no restrictions on the remaining element. The first three conditions are already met, and, since the 1 in the second row and third column is not a leading 1, it does not restrict the other entries in the third column.
It follows that there are infinitely many ways to fill the first row in.
Example Question #1 : Row Operations And Equivalent Systems
Which matrix is equivalent to
By adding 
Example Question #1 : Row Operations And Equivalent Systems
Which matrix is equivalent to
By adding row one to row two we get
Example Question #2 : Row Operations And Equivalent Systems
Which matrix is equivalent to
We add row two to row one to get
Example Question #3 : Row Operations And Equivalent Systems
Example Question #624 : Linear Algebra
Example Question #5 : Row Operations And Equivalent Systems
Example Question #4 : Row Operations And Equivalent Systems
Example Question #7 : Row Operations And Equivalent Systems
All Linear Algebra Resources
