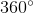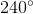All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #1 : How To Find The Angle Of Clock Hands
The clock in the classroom reads 5:00pm. What is the angle that the hands are forming?
Since the clock is a circle, you can determine that the total number of degrees inside the circle is 360. Since a clock has 12 numbers, we can divide 360 by 12 to see what the angle is between two numbers that are right next to each other. Thus, we can see that the angle between two numbers right next to each other is 

Example Question #1 : Circles
The time on a clock reads 5:00. What is the measure of the central angle formed by the hands of the clock?
First, remember that the number of degrees in a circle is 360. Then, figure out how many degrees are in between each number on the face of the clock. Since there are 12 numbers, there are 

Example Question #2 : Circles

Refer to the above figure. Which is the greater quantity?
(a)
(b) 3
(a) is the greater quantity
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
(b) is the greater quantity
If two chords intersect inside a circle, both chords are cut in a way such that the products of the lengths of the two chords formed in each are the same - in other words,
or
Therefore, 
Example Question #131 : Geometry

Figure NOT drawn to scale
In the above figure, 


Which is the greater quantity?
(a)
(b) 25
(a) is the greater quantity
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
(a) and (b) are equal



and 



The length hypotenuse, 

Example Question #135 : Geometry

Figure NOT drawn to scale.
Refer to the above figure. Which is the greater quantity?
(a)
(b) 7
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
(a) is the greater quantity
(b) is the greater quantity
If two chords intersect inside a circle, both chords are cut in a way such that the products of the lengths of the two chords formed in each are the same - in other words,
Solving for 
Since 


Example Question #2 : Chords

In the above figure, 
Which is the greater quantity?
(a)
(b) 32
(b) is the greater quantity
(a) and (b) are equal
It is impossible to determine which is greater from the information given
(a) is the greater quantity
(b) is the greater quantity
If a secant segment and a tangent segment are constructed to a circle from a point outside it, the square of the distance to the circle along the tangent is equal to the product of the distances to the two points on the circle along the secant; in other words,
Simplifying, then solving for 
To compare 



it follows that

Example Question #136 : Geometry

Figure NOT drawn to scale
In the above figure, 
Which is the greater quantity?
(a)
(b) 8
(a) is the greater quantity
It is impossible to determine which is greater from the information given
(b) is the greater quantity
(a) and (b) are equal
(a) and (b) are equal
If a secant segment and a tangent segment are constructed to a circle from a point outside it, the square of the distance to the circle along the tangent is equal to the product of the distances to the two points on the circle intersected by the secant; in other words,
Simplifying and solving for 
Factoring out 
Either 



Example Question #141 : Geometry

Refer to the above figure. Which is the greater quantity?
(a)
(b)
(a) and (b) are equal
It is impossible to determine which is greater from the information given
(b) is the greater quantity
(a) is the greater quantity
(a) and (b) are equal
If two chords intersect inside a circle, both chords are cut in a way such that the products of the lengths of the two chords formed in each are the same - in other words,
Divide both sides of this equation by 
The two quantities are equal.
Example Question #1 : How To Find The Length Of A Radius
The area of Circle B is four times that of Circle A. The area of Circle C is four times that of Circle B. Which is the greater quantity?
(a) Twice the radius of Circle B
(b) The sum of the radius of Circle A and the radius of Circle C
It cannot be determined from the information given.
(a) is greater.
(a) and (b) are equal.
(b) is greater.
(b) is greater.
Let 

The area of Circle B is 

(a) Twice the radius of circle B is 
(b) The sum of the radii of Circles A and B is 
This makes (b) greater.
Example Question #141 : Plane Geometry
The time is now 1:45 PM. Since noon, the tip of the minute hand of a large clock has moved 


Every hour, the tip of the minute hand travels the circumference of a circle. Between noon and 1:45 PM, one and three-fourths hours pass, so the tip travels 




Set this equal to 

This is equivalent to 1 foot 4 inches.
Certified Tutor
Certified Tutor
All ISEE Upper Level Quantitative Resources