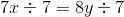All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #3 : How To Find The Area Of A Parallelogram

Figure NOT drawn to scale
The above figure shows Rhombus 



Give the area of Rhombus 
A rhombus, by definition, has four sides of equal length. Therefore, 


We will assign 
Also, both 


The figure, with the lengths, is below.

Rectangle 


The area of the entire Rhombus 



Example Question #261 : Geometry

In the above parallelogram, 
(A) The perimeter of the parallelogram
(B) 46 inches
(A) and (B) are equal
(B) is greater
It is impossible to determine which is greater from the information given
(A) is greater
(A) and (B) are equal
The measure of 

making the quantities equal.
Example Question #262 : Geometry
Parallelogram A is below:

Parallelogram B is below:

Note: These figures are NOT drawn to scale.
Refer to the parallelograms above. Which is the greater quantity?
(A) The perimeter of parallelogram A
(B) The perimeter of parallelogram B
(A) and (B) are equal
(B) is greater
(A) is greater
It is impossible to determine which is greater from the information given
(A) is greater
The perimeter of a parallelogram is the sum of its sidelengths; its height is irrelevant. Also, opposite sides of a parallelogram are congruent.
The perimeter of parallelogram A is

The perimeter of parallelogram B is

(A) is greater.
Example Question #263 : Plane Geometry

Figure NOT drawn to scale.
The above figure depicts Rhombus 


Give the perimeter of Rhombus 
All four sides of a rhombus have the same length, so we can find the perimeter of Rhombus 


Note that the length of 
Example Question #263 : Geometry
In Parallelogram 


(A)
(B)
It cannot be determined which of (a) and (b) is greater
(a) and (b) are equal
(b) is the greater quantity
(a) is the greater quantity
It cannot be determined which of (a) and (b) is greater
In Parallelogram 






Example Question #3 : Parallelograms
Which of the following can be the measures of the four angles of a parallelogram?
Opposite angles of a parallelogram must have the same measure, so the correct choice must have two pairs, each of the same angle measure. We can therefore eliminate 

Also, the sum of the measures of the angles of any quadrilateral must be 





Example Question #5 : Parallelograms

Refer to the above figure, which shows a parallelogram. What is 
Not enough information is given to answer this question.
The sum of two consecutive angles of a parallelogram is 
157 is the correct choice.
Example Question #267 : Plane Geometry
In Parallelogram 


Which is the greater quantity?
(a)
(b)
It cannot be determined which of (a) and (b) is greater
(b) is the greater quantity
(a) is the greater quantity
(a) and (b) are equal
(b) is the greater quantity
In Parallelogram 


Both are positive, so 
Example Question #268 : Plane Geometry
In Rhombus 


(A)
(B)
It cannot be determined which of (a) and (b) is greater
(b) is the greater quantity
(a) and (b) are equal
(a) is the greater quantity
(a) is the greater quantity
The four sides of a rhombus, by defintion, have equal length, so
Since 

Example Question #1 : Rhombuses
A rhombus has diagonals of length two and one-half feet and six feet. Which is the greater quantity?
(A) The perimeter of the rhombus
(B) Four yards
(A) is greater
(A) and (B) are equal
(B) is greater
It is impossible to determine which is greater from the information given
(A) is greater
It will be easier to look at these measurements as inches for the time being:


The diagonals of a rhombus are each other's perpendicular bisector, so, as can be seen in the diagram below, one side of a rhombus and one half of each diagonal form a right triangle. If we let 

By the Pythagorean Theorem,

Each side of the rhombus measures 39 inches, and its perimeter is

Four yards is equal to 
All ISEE Upper Level Quantitative Resources