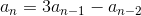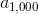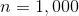Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Quantitative : Data Analysis

Study concepts, example questions & explanations for ISEE Upper Level Quantitative

Create An Account

All ISEE Upper Level Quantitative Resources

8 Diagnostic Tests 234 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #38 : Sets

Define a sequence as follows:

$a_{1} = 3$ $\displaystyle a_{1} = 3$

$a_{2} = 1$ $\displaystyle a_{2} = 1$

For all integers n > 2 $\displaystyle n > 2$, $a_{n} = 3a_{n-1} - a_{n-2}$ $\displaystyle a_{n} = 3a_{n-1} - a_{n-2}$.

Which of the following expressions is equal to $a_{1,000}$ $\displaystyle a_{1,000}$ ?

Possible Answers:

$8a_{998 } - 3 a_{997}$ $\displaystyle 8a_{998 } - 3 a_{997}$

$8a_{998 } - a_{997}$ $\displaystyle 8a_{998 } - a_{997}$

$9a_{998 } - 2a_{997}$ $\displaystyle 9a_{998 } - 2a_{997}$

$9a_{998 } - a_{997}$ $\displaystyle 9a_{998 } - a_{997}$

$a_{998 } -9a_{997}$ $\displaystyle a_{998 } -9a_{997}$

Correct answer:

$8a_{998 } - 3 a_{997}$ $\displaystyle 8a_{998 } - 3 a_{997}$

Explanation:

Setting $\displaystyle n = 1,000$:

$a_{n} = 3a_{n-1} - a_{n-2}$ $\displaystyle a_{n} = 3a_{n-1} - a_{n-2}$

$a_{1,000} = 3a_{1,000-1} - a_{1,000-2}$ $\displaystyle a_{1,000} = 3a_{1,000-1} - a_{1,000-2}$

$a_{1,000} = 3a_{999} - a_{998}$ $\displaystyle a_{1,000} = 3a_{999} - a_{998}$

Similarly,

$a_{999} = 3a_{998 } - a_{997}$ $\displaystyle a_{999} = 3a_{998 } - a_{997}$

Substituting:

$a_{1,000} = 3 (3a_{998 } - a_{997}) - a_{998}$ $\displaystyle a_{1,000} = 3 (3a_{998 } - a_{997}) - a_{998}$

$=9a_{998 } - 3 a_{997} - a_{998}$ $\displaystyle =9a_{998 } - 3 a_{997} - a_{998}$

$=8a_{998 } - 3 a_{997}$ $\displaystyle =8a_{998 } - 3 a_{997}$

Report an Error

View Tutors

Dehlly
Certified Tutor

Universidad Nacional de Colombia, Bachelor in Business Administration, Mathematics and Statistics. Columbia University in th...

View Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

All ISEE Upper Level Quantitative Resources

8 Diagnostic Tests 234 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Phoenix, Chemistry Tutors in Washington DC, Algebra Tutors in Chicago, Reading Tutors in Denver, LSAT Tutors in San Francisco-Bay Area, GMAT Tutors in Dallas Fort Worth, MCAT Tutors in Miami, French Tutors in Houston, French Tutors in San Diego, Statistics Tutors in San Francisco-Bay Area

Popular Courses & Classes

LSAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Denver, SSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Denver, Spanish Courses & Classes in Atlanta, Spanish Courses & Classes in Philadelphia, GMAT Courses & Classes in Chicago, GRE Courses & Classes in Miami, MCAT Courses & Classes in Chicago, SSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ACT Test Prep in Philadelphia, SSAT Test Prep in Washington DC, MCAT Test Prep in Philadelphia, SAT Test Prep in Phoenix, LSAT Test Prep in Seattle, ISEE Test Prep in New York City, GMAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Phoenix, LSAT Test Prep in Chicago, GRE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Quantitative : Data Analysis

Study concepts, example questions & explanations for ISEE Upper Level Quantitative

All ISEE Upper Level Quantitative Resources

Example Questions

Example Question #38 : Sets

All ISEE Upper Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: