All ISEE Upper Level Math Resources
Example Questions
Example Question #1 : How To Find The Volume Of A Cube
If a cube is inches tall, what is its volume?
Not enough information provided.
To find the volume of a cube, we multiply length by width by height, which can be represented with the forumla . Since a cube has equal sides, we can use for all three values.
Example Question #1 : How To Find The Volume Of A Cube
What is the volume of a cube with a side length equal to inches?
The volume of a a cube (or rectangular prism) can be solved using the following equation:
Example Question #931 : Grade 7
Give the volume of a cube with surface area 150 square inches.
Let be the length of one edge of the cube. Since its surface area is 150 square inches, one face has one-sixth of this area, or square inches. Therefore, , and .
The volume is the cube of this, or cubic inches.
Example Question #1 : How To Find The Volume Of A Cube
What is the volume of a cube in which the edge is equal to , and the value of is:
First, the value of x must be solved for:
Given the edge of the cube is , plugging in the value of x results in . Thus, the area would be equal to this value cubed, which would result in 62.
Thus, 62 is the correct answer.
Example Question #2 : How To Find The Volume Of A Cube
The length of a diagonal of one face of a cube is . Give the volume of the cube.
Since a diagonal of a square face of the cube is, each side of each square has length .
Cube this to get the volume of the cube:
Example Question #2 : Cubes
The distance from one vertex of a perfectly cubic aquarium to its opposite vertex is 1.5 meters. Give the volume of the aquarium in liters.
1 cubic meter = 1,000 liters.
The correct answer is not given among the other responses.
The correct answer is not given among the other responses.
Let be the length of one edge of the cube. By the three-dimensional extension of the Pythagorean Theorem,
meters.
Cube this sidelength to get the volume:
cubic meters.
To convert this to liters, multiply by 1,000:
liters.
This is not among the given responses.
Example Question #3 : How To Find The Volume Of A Cube
Give the volume of a cube with surface area 240 square inches.
Let be the length of one edge of the cube. Since its surface area is 240 square inches, one face has one-sixth of this area, or square inches. Therefore, , and .
The volume is the cube of this, or cubic inches.
Example Question #1 : How To Find The Volume Of A Cube
An aquarium is shaped like a perfect cube; the perimeter of each glass face is meters. If it is filled to the recommended capacity, then, to the nearest hundred cubic liters, how much water will it contain?
Insufficient information is given to answer the question.
Note:
A perfect cube has square faces; if a face has perimeter meters, then each side of each face measures one fourth of this, or meters. The volume of the tank is the cube of this, or
cubic meters.
Its capacity in liters is liters.
of this is
liters.
This rounds to liters, the correct response.
Example Question #21 : Solid Geometry
Your friend gives you a puzzle cube for your birthday. If the length of one edge is 5cm, what is the volume of the cube?
Your friend gives you a puzzle cube for your birthday. If the length of one edge is 5cm, what is the volume of the cube?
To find the volume of a cube, use the following formula:
Where s is the side length.
Plug in what we know to get our answer:
Example Question #331 : Isee Upper Level (Grades 9 12) Mathematics Achievement
A cube has a side length of , what is the volume of the cube?
A cube has a side length of , what is the volume of the cube?
To find the volume of a cube, use the following formula:
Plug in our known side length and solve
Making our answer:
Certified Tutor
Certified Tutor
All ISEE Upper Level Math Resources










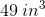

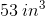













![\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/200393/gif.latex)










![\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/200399/gif.latex)
![\sqrt[3]{62}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/200400/gif.latex)
































































