We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : Parallelograms

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #271 : Geometry

Parallelogram2

Give the area of the above parallelogram if BC = 10 .

Possible Answers:

$25\sqrt{3}$

$50\sqrt{2}$

$25\sqrt{2}$

Correct answer:

$25\sqrt{3}$

Explanation:

Multiply height by base to get the area.

By the 30-60-90 Theorem:

$BD = \frac{BC}{2} = \frac{10}{2}} = 5$

and

$CD =BD \cdot \sqrt{3} = 5\sqrt{3}$

The area is therefore

$BD \cdot CD = 5 \cdot 5\sqrt{3} = 25\sqrt{3}$

Report an Error

Example Question #281 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Parallelogram1

Give the area of the above parallelogram if BC = 10 .

Possible Answers:

$50\sqrt{3}$

$25\sqrt{3}$

$25\sqrt{2}$

$50\sqrt{2}$

Correct answer:

Explanation:

Multiply height by base to get the area.

By the 45-45-90 Theorem,

$BD = CD = \frac{BC}{\sqrt{2}} = \frac{10}{\sqrt{2}}$ .

The area is therefore

$BD \cdot CD = \frac{10}{\sqrt{2}} \cdot \frac{10}{\sqrt{2}} = \frac{100}{2} = 50$

Report an Error

Example Question #3 : How To Find The Area Of A Parallelogram

Three of the vertices of a parallelogram on the coordinate plane are (0,0), (9,12),(12,9) . What is the area of the parallelogram?

Possible Answers:

Insufficient information is given to answer the problem.

Correct answer:

Explanation:

As can be seen in the diagram, there are three possible locations of the fourth point of the parallelogram:

Axes_2

Regardless of the location of the fourth point, however, the triangle with the given three vertices comprises exactly half the parallelogram. Therefore, the parallelogram has double that of the triangle.

The area of the triangle can be computed by noting that the triangle is actually a part of a 12-by-12 square with three additional right triangles cut out:

Axes_1

The area of the 12 by 12 square is $12^{2} = 144$

The area of the green triangle is $\frac{1}{2} \times 12 \times 9 = 54$ .

The area of the blue triangle is $\frac{1}{2} \times 9 \times 12 = 54$ .

The area of the pink triangle is $\frac{1}{2} \times 3 \times 3 = 4 \frac{1}{2}$ .

The area of the main triangle is therefore

$144- 54-54-4\frac{1}{2} = 31\frac{1}{2}$

The parallelogram has area twice this, or $2 \times 31\frac{1}{2} = 63$ .

Report an Error

Example Question #1 : Parallelograms

One of the sides of a square on the coordinate plane has an endpoint at the point with coordinates (4, 5 ) ; it has the origin as its other endpoint. What is the area of this square?

Possible Answers:

Correct answer:

Explanation:

The length of a segment with endpoints (0,0) and (4, 5 ) can be found using the distance formula with $x_{1} = y_{1} = 0$ , $x_{2} = 4$ , $y_{2} = 5$ :

$d = \sqrt{(x_{2}- x_{1})^{2}+(y_{2}-y_{1})^{2}}$

$= \sqrt{(4-0)^{2}+(5-0 )^{2}}$

$= \sqrt{4^{2}+5^{2}}$

$= \sqrt{16+25 }$

$= \sqrt{41}$

This is the length of one side of the square, so the area is the square of this, or 41.

Report an Error

Example Question #1 : How To Find The Perimeter Of A Parallelogram

Parallelogram1

The area of the Parallelogram ABCD is . Give its perimeter in terms of .

Possible Answers:

$4 \sqrt{2X}$

$\sqrt{6X}$

$2 \sqrt{3X}$

$2 \sqrt{X} + 2 \sqrt{2X}$

$4 \sqrt{X }$

Correct answer:

$2 \sqrt{X} + 2 \sqrt{2X}$

Explanation:

The height of the parallelogram is , and the base is . By the 45-45-90 Theorem, BD=CD . Since the product of the height and the base of a parallelogram is its area,

$BD \cdot CD = A$

$\left (BD \right )^{2} = X$

$BD = \sqrt{X}$

Also by the 45-45-90 Theorem,

$CD = AB = BD = \sqrt{X}$ , and

$AD = BC = \sqrt{X} \cdot \sqrt{2} = \sqrt{2X}$

The perimeter of the parallelogram is

$AB + CD + BC + AD = \sqrt{X} + \sqrt{X} + \sqrt{2X}+ \sqrt{2X} = 2 \sqrt{X} + 2 \sqrt{2X}$

Report an Error

Example Question #1 : How To Find The Perimeter Of A Parallelogram

Parallelogram1

Calculate the perimeter of the above parallelogram if $BD = 8\sqrt{2}$ .

Possible Answers:

$48\sqrt{2}$

$16+ 16 \sqrt{2}$

$32+ 16 \sqrt{2}$

$32+ 32\sqrt{2}$

Correct answer:

$32+ 16 \sqrt{2}$

Explanation:

By the 45-45-90 Theorem,

$AB= CD = BD = 8\sqrt{2}$

$AD= BC = BD \cdot \sqrt{2} = 8\sqrt{2} \cdot \sqrt{2} = 8 \cdot 2 = 16$

The perimeter of the parallelogram is

$AB + CD + BC + AD = 8 \sqrt{2} + 8 \sqrt{2} + 16+16 = 32+ 16 \sqrt{2}$

Report an Error

Example Question #5 : Parallelograms

Parallelogram2

Calculate the perimeter of the above parallelogram if $BD = 30\sqrt{6}$ .

Possible Answers:

$360\sqrt{2}$

$180\sqrt{2}$

$240+120\sqrt{2}$

360

$180+180\sqrt{2}$

Correct answer:

$180\sqrt{2}$

Explanation:

By the 30-60-90 Theorem:

$AB = CD= \frac{BD}{\sqrt{3}} = \frac{30 \sqrt{6}}{\sqrt{3}}= 30\sqrt{2}$ , and

$BC = AD = 2\cdot AB = 2 \cdot 30\sqrt{2} =60\sqrt{2}$

The perimeter of the parallelogram is

$AB + CD + BC + AD = 30\sqrt{2}+ 30\sqrt{2}+60\sqrt{2}+60\sqrt{2}= 180\sqrt{2}$

Report an Error

Example Question #284 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Find the perimeter of a parallelogram with a base of 6in and a side of length 8in.

Possible Answers:

$32\text{in}$

$48\text{in}$

$28\text{in}$

$36\text{in}$

$24\text{in}$

Correct answer:

$28\text{in}$

Explanation:

A parallelogram has 4 sides. A base (where the opposite side is equal) and a side (where the opposite side is equal). So, we will use the following formula:

P = b+b+s+s

where b is the base and s is the side of the parallelogram.

We know the base has a length of 6in. We also know the side has a length of 8in.

Knowing this, we can substitute into the formula. We get

$P = 6\text{in} + 6\text{in} + 8\text{in} + 8\text{in}$

$P = 28\text{in}$

Report an Error

Example Question #282 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Solve for :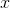

Problem_10

Possible Answers:

x=95

x=89

x=109

x=19

Correct answer:

x=109

Explanation:

Find the sum of the interior angles of the polygon using the following equation where n is equal to the number of sides.

=180(n-2)

180(4-2)=180(2)=360

The sum of the angles must equal 360.

360=x+71+x+71=2x+142

360-142=2x+142-142

218=2x

109=x

Report an Error

View Tutors

Evgenii
Certified Tutor

View Tutors

Pavan
Certified Tutor

University of Tennessee, Knoxville, Master's/Graduate, Mechanical Engineering. Pennsylvania State University, Master's/Gradua...

View Tutors

Omar
Certified Tutor

Arizona State University, Bachelors, Civil Engineering.

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Dallas Fort Worth, English Tutors in San Diego, ISEE Tutors in Miami, Spanish Tutors in Chicago, GMAT Tutors in Houston, LSAT Tutors in Chicago, LSAT Tutors in Houston, ACT Tutors in Philadelphia, MCAT Tutors in Atlanta, Reading Tutors in New York City

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Los Angeles, SSAT Courses & Classes in San Diego, LSAT Courses & Classes in New York City, SSAT Courses & Classes in Miami, MCAT Courses & Classes in Miami, ACT Courses & Classes in Philadelphia, GRE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Washington DC

Popular Test Prep

SSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Denver, SSAT Test Prep in Los Angeles, SSAT Test Prep in New York City, LSAT Test Prep in Philadelphia, ACT Test Prep in Philadelphia, SAT Test Prep in Dallas Fort Worth, ACT Test Prep in Dallas Fort Worth, MCAT Test Prep in Seattle, ISEE Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : Parallelograms

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #271 : Geometry

Example Question #281 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #3 : How To Find The Area Of A Parallelogram

Example Question #1 : Parallelograms

Example Question #1 : How To Find The Perimeter Of A Parallelogram

Example Question #1 : How To Find The Perimeter Of A Parallelogram

Example Question #5 : Parallelograms

Example Question #284 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #282 : Isee Upper Level (Grades 9 12) Mathematics Achievement

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: