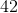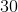Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : Data Analysis and Probability

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 … 7 8 9 10 11 12 13 14 15 Next →

Example Question #131 : Data Analysis

Over the course of seven games, Joanna scored the following number of points for her high school's varsity basketball team:

14, 20, 12, 9, 10, 8, 12 .

What is the range of the number of points she scored?

Possible Answers:

Correct answer:

Explanation:

In order to find the range, you must first identify the smallest and the largest number of the set.

The smallest number of the set is , while the largest number is .

Take the difference between these two to find the range.

$\text{Range}=20-8=12$

Report an Error

Example Question #132 : Data Analysis

Use the following data set to answer the question:

9, 4, 5, 7, 3, 6, 5, 8, 6, 3, 5

Find the range.

Possible Answers:

Correct answer:

Explanation:

To find the range of a data set, we will find the smallest number and the largest number. Then, we will find the difference of those two numbers.

So, given the set

9, 4, 5, 7, 3, 6, 5, 8, 6, 3, 5

we can see the smallest number is 3 and the largest number is 9. Now, we will find the difference.

9-3=6

Therefore, the range of the data set is 6.

Report an Error

Example Question #133 : Data Analysis

Use the following data set to answer the question:

5, 4, 7, 6, 9, 6, 2, 6, 9

Find the range.

Possible Answers:

Correct answer:

Explanation:

To find the range of a data set, we will find the smallest number and the largest number. Then, we will find the difference of those two numbers.

So, given the set

5, 4, 7, 6, 9, 6, 2, 6, 9

we can see the smallest number is 2 and the largest number is 9. Now, we will find the difference.

9-2=7

Therefore, the range of the data set is 7.

Report an Error

Example Question #134 : Data Analysis

Determine the range: [-1,-3,-5,21,-21]

Possible Answers:

$\frac{9}{5}$

Correct answer:

Explanation:

The range is the difference between the largest and smallest numbers.

The largest number is:

The smallest number is:

Subtract both quantities.

21-(-21) = 21+21 = 42

The answer is:

Report an Error

Example Question #1 : How To Find The Missing Part Of A List

Define set $A = \left \{ 1, 2, 4, 8, 10, a, g, j, r, w \right \}$ . Which of the following sets could we define to be set so that $A \cap B = \varnothing$ ?

Possible Answers:

$B = \left \{ 3, 5, 6, 7, 9, e, g, t, u, x\right \}$

$B =\left \{ 3, 5, 7, 10, 13, e, f, h, k, y \right \}$

$B = \left \{ 5,6,7,11,17, f,h,i,k,r\right \}$

$B = \left \{ 3, 6, 7, 9, 12, b, e, h, s, t\right \}$

$B= \left \{ 3,5, 6,8,14,d,f,s,t,x\right \}$

Correct answer:

$B = \left \{ 3, 6, 7, 9, 12, b, e, h, s, t\right \}$

Explanation:

For $A \cap B = \varnothing$ to be a true statement, sets and cannot have any elements in common. We can eliminate four of these choices of by noting that in each, there is one element (underlined) also in :

$\left \{ 3,5, 6,\underline{8},14,d,f,s,t,x\right \}$

$\left \{ 3, 5, 7, \underline{10}, 13, e, f, h, k, y \right \}$

$\left \{ 3, 5, 6, 7, 9, e, \underline{g}, t, u, x\right \}$

$\left \{ 5,6,7,11,17, f,h,i,k,\underline{r}\right \}$

However, $B = \left \{ 3, 6, 7, 9, 12, b, e, h, s, t\right \}$ shares no elements with $A = \left \{ 1, 2, 4, 8, 10, a, g, j, r, w \right \}$ , so their intersection is $\varnothing$ by definition. This is the correct choice.

Report an Error

Example Question #2 : How To Find The Missing Part Of A List

Given a set $A = \left \{ 1,3, 6, 7, 8\right \}$ , which of the following sets could we assign to such that $A \cup B = \left \{ 1,2, 3, 4, 5, 6, 7, 8, 9, 10\right \}$ ?

Possible Answers:

$\left \{ 6,5,4, 9, 10\right \}$

$\left \{ 2, 4, 9, 10 \right \}$

$\left \{1, 2, 4, 5, 6, 9, 10, 12\right \}$

$\left \{ 2, 9,5, 4, 10, 8\right \}$

None of the choices answer the question correctly.

Correct answer:

$\left \{ 2, 9,5, 4, 10, 8\right \}$

Explanation:

$A \cup B$ is the union of the sets, i.e. the set of all elements in , , or both.

For $A \cup B = \left \{ 1,2, 3, 4, 5, 6, 7, 8, 9, 10\right \}$ , must include all elements in $\left \{ 1,2, 3, 4, 5, 6, 7, 8, 9, 10\right \}$ that are not in , or $\left \{ 2, 4, 5, 9, 10\right \}$ . This allows us to eliminate $\left \{ 2, 4, 9, 10 \right \}$ , which excludes 5, and $\left \{ 6,5,4, 9, 10\right \}$ , which excludes 2.

Also, cannot include any element not in $\left \{ 1,2, 3, 4, 5, 6, 7, 8, 9, 10\right \}$ . This allows us to eliminate $\left \{1, 2, 4, 5, 6, 9, 10, 12\right \}$ , which includes 12.

This leaves $\left \{ 2, 9,5, 4, 10, 8\right \}$ .

If $B = \left \{ 2, 9,5, 4, 10, 8\right \}$ , then

$A \cup B =\left \{ 1,3, 6, 7, 8\right \} \cup \left \{ 2, 9,5, 4, 10, 8\right \}$

$= \left \{ 1,2, 3, 4, 5, 6, 7, 8, 9, 10\right \}$ .

This is the correct choice.

Report an Error

Example Question #3 : How To Find The Missing Part Of A List

Examine the sequence:

$5, 6, 8, 11, 15, 20, 26, \square, \bigcirc,...$

What number goes into the circle?

Possible Answers:

Correct answer:

Explanation:

Each element is obtained by adding a number to the previous one; the number added increases by 1 each time:

5 + 1 = 6

6 + 2 = 8

8 + 3 = 11

11 + 4 = 15

15 + 5 = 20

20 + 6 = 26

26 + 7 = 33 - this number replaces the square

33 + 8 = 41 - this number replaces the circle

Report an Error

Example Question #4 : How To Find The Missing Part Of A List

A pair of fair dice are tossed. What is the probability that the product of the numbers of the faces is greater than or equal to ?

Possible Answers:

$\frac {1}{6}$

$\frac {5}{18}$

$\frac {1}{3}$

$\frac {1}{4}$

$\frac {2}{9}$

Correct answer:

$\frac {2}{9}$

Explanation:

Out of a possible thirty-six rolls, the following result in a product of twenty or greater:

$\left\{ (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6) \right\}$

This is eight out of thirty-six, making the probability

$\frac{8}{36} = \frac {2}{9}$ .

Report an Error

Example Question #5 : How To Find The Missing Part Of A List

Ten students are running for student council; each member of the student body will choose four.

Two of the candidates are Kevin's brothers, Mickey and Steve. Kevin wants to vote for one, but not both, of his brothers. How many ways can Kevin fill out his ballot so that he can vote for exactly one of his brothers?

Possible Answers:

112

672

336

224

Correct answer:

112

Explanation:

Kevin will choose three students from the eight who are not his brothers, and will do so without respect to order. This is the number of combinations of three from eight:

$C(8,3) = \frac{8!}{(8-3)!\; 3!} = \frac{8!}{5!\; 3!} = \frac{40,320}{120 \times 6} = 56$

Kevin will also choose one of his two brothers. By the multiplication principle, Kevin has $56 \times 2 = 112$ ways to fill out the ballot.

Report an Error

Example Question #6 : How To Find The Missing Part Of A List

Define $f (x) = \frac{1}{x ^{2}+ 9 }$

What is the natural domain of ?

Possible Answers:

$(-\infty , 3) \cup (3 , \infty)$

$(-\infty ,3)$

$(3 , \infty)$

$(-\infty , \infty)$

Correct answer:

$(-\infty , \infty)$

Explanation:

The only possible restriction of the domain here is the denominator $x ^{2}+ 9$ , which cannot be equal to 0. We can find any such values of as follows:

$x ^{2}+ 9 = 0$

$x ^{2}+ 9- 9 = 0 - 9$

$x ^{2} = - 9$

This has no real solution, so the domain is the set of all real numbers, $(-\infty , \infty)$ .

Report an Error

← Previous 1 2 … 7 8 9 10 11 12 13 14 15 Next →

View Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View Tutors

Pushpendra
Certified Tutor

university of allahabad, Bachelor of Science, Mathematics.

View Tutors

Jaroslaw
Certified Tutor

Heriot Watt University, Master of Science, Physics. Heriot Watt University, Doctor of Science, Theoretical and Mathematical P...

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Los Angeles, MCAT Tutors in Philadelphia, SSAT Tutors in Phoenix, ACT Tutors in Miami, French Tutors in Seattle, Physics Tutors in Houston, SSAT Tutors in Atlanta, SAT Tutors in Denver, SSAT Tutors in Boston, GRE Tutors in Atlanta

Popular Courses & Classes

MCAT Courses & Classes in Philadelphia, GRE Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Atlanta, GMAT Courses & Classes in Los Angeles, GRE Courses & Classes in Denver, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in Washington DC, Spanish Courses & Classes in Miami, ACT Courses & Classes in Phoenix, SAT Courses & Classes in Philadelphia

Popular Test Prep

SAT Test Prep in San Diego, LSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Miami, ISEE Test Prep in Los Angeles, ACT Test Prep in Phoenix, GRE Test Prep in Los Angeles, SAT Test Prep in Phoenix, MCAT Test Prep in Washington DC, MCAT Test Prep in Denver, GMAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : Data Analysis and Probability

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #131 : Data Analysis

Example Question #132 : Data Analysis

Example Question #133 : Data Analysis

Example Question #134 : Data Analysis

Example Question #1 : How To Find The Missing Part Of A List

Example Question #2 : How To Find The Missing Part Of A List

Example Question #3 : How To Find The Missing Part Of A List

Example Question #4 : How To Find The Missing Part Of A List

Example Question #5 : How To Find The Missing Part Of A List

Example Question #6 : How To Find The Missing Part Of A List

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: