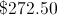ISEE Middle Level Quantitative : Whole and Part
Study concepts, example questions & explanations for ISEE Middle Level Quantitative
All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #1 : How To Find The Part From The Whole
Harvey bought a suit at a 25% employee discount at the store where he works. The suit originally cost $350.00. How much did he end up paying?
Finding 25% of a number is the same as multiplying it by 0.25; to get the discount, multiply 0.25 by the original purchase price of $350.00
To get the price Harvey paid, subtract the discount from the original price:
Example Question #2 : How To Find The Part From The Whole
Which of the following is true if 
Two expressions are equivalent in modulo 9 arithmetic if and only if, when each is divided by 9, the same remainder is yielded.
so
Example Question #3 : How To Find The Part From The Whole
(a) The remainder if 
(b) The remainder if 
(a) is the greater quantity
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
It is impossible to determine which is greater from the information given
The information is insufficient.
For example, if 
This gives the division in (b) the greater remainder.
But if 
This gives the division in (a) the greater remainder.
Example Question #4 : How To Find The Part From The Whole
(a) The remainder if 
(b) The remainder if 
(a) is the greater quantity
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
(a) and (b) are equal
Since 
Also,
The two remainders are both equal to 0.
Example Question #5 : How To Find The Part From The Whole
(a) The remainder if
(b) The remainder if 
(a) and (b) are equal
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) is the greater quantity
(a) is the greater quantity
If 
Example Question #1 : Whole And Part
150% of what number is 9,000?
Taking 150% of a number is the same as multiplying that number by 1.5. We can find our number, therefore, by dividing 9,000 by 1.5:
Example Question #2 : How To Find The Whole From The Part
If the remainder of dividing 
Suppose we call 
If the remainder is 1, then
This leaves 2, which can be the remainder; for example, 8, which is a multiple of 2, but not a multiple of 6, yields a quotient of 1 and a remainder of 2 when divided by 2.
All ISEE Middle Level Quantitative Resources
