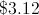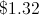Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Middle Level Quantitative : ISEE Middle Level (grades 7-8) Quantitative Reasoning

Study concepts, example questions & explanations for ISEE Middle Level Quantitative

Create An Account

All ISEE Middle Level Quantitative Resources

6 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Equations

Choose the best answer from the four choices given.

Richard reaches into his pocket and determines that he has $3.85 in quarters and nickels. When he pulls out his fistful of change, though, he is dismayed to realize that what he thought were quarters are really pennies and what he thought to be nickels are really dimes. If he has 12 pennies, how much is his change worth?

Possible Answers:

$\$1.32$

$\$3.12$

$\$3.02$

$\$1.82$

Correct answer:

$\$1.82$

Explanation:

If Richard has 12 pennies, that means that he thought he had 12 quarters ($3.00) and 85 cents worth of nickels (17 nickels). Since what he thought were nickels are really dimes, it means that he has $1.70 worth of dimes to go along with his 12 cents in pennies.

$\$1.70+\$0.12=\$1.82$

Report an Error

Example Question #3 : How To Find The Solution To An Equation

Using the information given in each question, compare the quantity in Column A to the quantity in Column B.

5y-9x=10

Column A Column B

the slope of the y-intercept

this equation of this equation

Possible Answers:

The relationship cannot be determined from the information given.

The quantity in Column B is greater.

The two quantities are equal.

The quantity in Column A is greater.

Correct answer:

The quantity in Column B is greater.

Explanation:

Divide each of the elements of the equation by 5 to get it into y=mx+b form.

$\frac{5y}{5}-\frac{9x}{5}=\frac{10}{5}$

$y-\frac{9}{5}x=2$

$y=\frac{9}{5}x+2$

Thus, the slope is 1.8 and the y-intercept is 2, so B is the correct answer.

Report an Error

Example Question #3 : How To Find The Solution To An Equation

x(3x-7)= 40

Which is the greater quantity?

(a)

(b)

Possible Answers:

It is impossible to tell from the information given

(a) and (b) are equal

(b) is greater

(a) is greater

Correct answer:

It is impossible to tell from the information given

Explanation:

Rewrite in standard form:

x(3x-7)= 40

$x \cdot 3x-x \cdot7 = 40$

$3x^{2}-7x = 40$

$3x^{2}-7x- 40 = 40 - 40$

$3x^{2}-7x- 40 = 0$

Use the -method to factor the quadratic expression, splitting the middle term using integers whose product is 3 (-40)= -120 and whose sum is . These two numbers are -15,8 , so the equation becomes:

$3x^{2}-15x+8x- 40 = 0$

$\left ( 3x^{2}-15x \right ) +\left ( 8x- 40 \right ) = 0$

$3x \left ( x-5 \right ) + 8 \left ( x-5 \right ) = 0$

$\left (3x+ 8 \right ) \left ( x-5 \right ) = 0$

Set each linear binomial to 0 and solve:

3x+ 8 = 0

3x+ 8 -8= 0 -8

3x= -8

$3x\div 3= -8 \div 3$

$x = -2 \frac{2}{3}$

x - 5 = 0

x - 5+ 5 = 0 + 5

x = 5

Therefore, it is not clear whether is greater than or less than 3.

Report an Error

Example Question #5 : How To Find The Solution To An Equation

$\left ( t- 10\right ) (2t-3) = -35$

Which is the greater quantity?

(a)

(b)

Possible Answers:

It is impossible to tell from the information given

(a) is greater

(a) and (b) are equal

(b) is greater

Correct answer:

(a) is greater

Explanation:

Rewrite in standard form:

$\left ( t- 10\right ) (2t-3) = -35$

$t \cdot 2t -t \cdot 3 -10 \cdot 2t + 10 \cdot 3 = -35$

$2t^{2} -3t -20 t + 30 = -35$

$2t^{2} -23t + 30 = -35$

$2t^{2} -23t + 30+ 35 = -35 + 35$

$2t^{2} -23t + 65 =0$

Use the -method to factor the quadratic expression, splitting the middle term using integers whose product is $2 \times65=130$ and whose sum is . These integers are -13,-10 , so the equation becomes:

$2t^{2} -10t - 13t + 65 =0$

Group and solve:

$\left ( 2t^{2} -10t \right )-\left ( 13t - 65 \right ) =0$

$2t \left ( t-5\right )-13\left ( t-5 \right ) =0$

$\left ( 2t -13 \right )\left ( t-5\right ) =0$

Set each linear binomial to 0 and solve:

2t-13 = 0

2t-13 +13= 0+13

2t = 13

$2t \div 2 = 13 \div 2$

$t = 6 \frac{1}{2}$

t - 5 = 0

t - 5+ 5 = 0 + 5

t = 5

In either case, t > 0 .

Report an Error

Example Question #8 : Equations

x(x+1)= 30

Which is the greater quantity?

(a)

(b)

Possible Answers:

(a) and (b) are equal

(a) is greater

It is impossible to tell from the information given

(b) is greater

Correct answer:

It is impossible to tell from the information given

Explanation:

Rewrite in standard form:

x(x+1)= 30

$x \cdot x+x \cdot 1 = 30$

$x ^{2}+x = 30$

$x ^{2}+x- 30 = 30 - 30$

$x ^{2}+x- 30 = 0$

Factor the quadratic expression as (x + ?)(x + ?) , replacing the question marks with two integers whose product is and whose sum is 1. These integers are -5,6 , so the equation becomes:

(x-5)(x+6)= 0

Set each linear binomial to 0 and solve:

$x-5= 0 \Rightarrow x= 5$

$x+ 6 = 0 \Rightarrow x = -6$

Therefore, it is not clear whether is greater than or less than 0.

Report an Error

Example Question #4 : How To Find The Solution To An Equation

y (y + 7) = 30

Which is the greater quantity?

(a)

(b)

Possible Answers:

It is impossible to tell from the information given

(a) is greater

(a) and (b) are equal

(b) is greater

Correct answer:

(b) is greater

Explanation:

Rewrite in standard form:

y (y + 7) = 30

$y \cdot y +y \cdot 7 = 30$

$y ^{2} +7y = 30$

$y ^{2} +7y- 30 = 30 - 30$

$y ^{2} +7y- 30 = 0$

Factor the quadratic expression as (y + ?)(y + ?) , replacing the question marks with two integers whose product is and whose sum is 7. These integers are -3,10 , so rewrite:

(y -3)(y+ 10) = 0

Set each linear binomial to 0 and solve:

$y- 3 \Rightarrow y= 3$

$y+10= 0 \Rightarrow y = -10$

Both solutions are less than 5.

Report an Error

Example Question #5 : How To Find The Solution To An Equation

$y^{2} + 50 = 15y$

Which is the greater quantity?

(a)

(b)

Possible Answers:

(a) and (b) are equal

(a) is greater

It is impossible to tell from the information given

(b) is greater

Correct answer:

It is impossible to tell from the information given

Explanation:

Rewrite in standard form:

$y^{2} + 50 = 15y$

$y^{2} + 50 -15y= 15y -15y$

$y^{2} -15y+ 50= 0$

Factor the quadratic expression as (y + ?)(y + ?) , replacing the question marks with two integers whose product is 50 and whose sum is . These integers are -5,-10 , so rewrite the equation as:

(y -5)(y-10) = 0

Set each linear binomial to 0 and solve:

$y -5= 0\Rightarrow y = 5$

$y -10= 0\Rightarrow y = 10$

It is unclear whether is equal to or greater than 5.

Report an Error

Example Question #11 : Equations

$\left (x-5 \right )^{2} = 36$

Which is the greater quantity?

(a)

(b)

Possible Answers:

It is impossible to tell from the information given

(a) and (b) are equal

(b) is greater

(a) is greater

Correct answer:

(a) is greater

Explanation:

Use the square root method to solve this equation:

$\left (x-5 \right )^{2} = 36$

$x-5 =- 6 \textrm{ or }x-5 = 6$

Solve each equation separately:

x-5 =- 6

x-5 +5=- 6 + 5

x = -1

x-5 = 6

x-5 +5= 6+5

x = 11

In either case, x > - 6

Report an Error

Example Question #132 : Isee Middle Level (Grades 7 8) Quantitative Reasoning

$\frac{x}{3}-9=11$

5y+5=100

Column A Column B
x y

Possible Answers:

There can be no relationship determined from the two quantities.

The quantities are equal.

The quantity in Column A is greater.

The quantity in Column B is greater.

Correct answer:

The quantity in Column A is greater.

Explanation:

First, off you need to find the quantities of x and y. For the first equation, add 9 to both sides so that $\frac{x}{3}=20.$ Multiply both sides by 3 so that x=60. Then, solve the second equation. First, subtract 5 from both sides so that 5y=95 . Divide both sides by 5 so that y=19. Therefore, the quantity in Column A is greater.

Report an Error

Example Question #131 : Isee Middle Level (Grades 7 8) Quantitative Reasoning

$\frac{x}{2}+7=19$

3y-14=7

Column A Column B

x y

Possible Answers:

There is no way to determine the relationship between the columns.

The quantity in Column B is greater.

The quantity in Column A is greater.

The quantities in each column are equal.

Correct answer:

The quantity in Column A is greater.

Explanation:

First, you must solve for x and y. To solve for x, first subtract 7 from both sides, so that you get $\frac{x}{2}=12$ . Multiply both sides by 2, giving you 24 for x. To solve for y, first add 14 to both sides, which gives you 3y=21. Divide both sides by 3 to give you 7. Therefore, Column A is greater.

Report an Error

View Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

All ISEE Middle Level Quantitative Resources

6 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Philadelphia, ISEE Tutors in Houston, Spanish Tutors in Seattle, Statistics Tutors in Washington DC, Math Tutors in Washington DC, SSAT Tutors in Atlanta, Computer Science Tutors in Phoenix, Computer Science Tutors in San Diego, Reading Tutors in Miami, GMAT Tutors in Dallas Fort Worth

Popular Courses & Classes

MCAT Courses & Classes in San Diego, GMAT Courses & Classes in Washington DC, Spanish Courses & Classes in Philadelphia, MCAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Atlanta, MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Miami, ACT Courses & Classes in New York City, ACT Courses & Classes in Houston, ACT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

GMAT Test Prep in Denver, ACT Test Prep in New York City, ACT Test Prep in Houston, LSAT Test Prep in Denver, ISEE Test Prep in Los Angeles, ACT Test Prep in Phoenix, ISEE Test Prep in Boston, GMAT Test Prep in Miami, LSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Middle Level Quantitative : ISEE Middle Level (grades 7-8) Quantitative Reasoning

Study concepts, example questions & explanations for ISEE Middle Level Quantitative

All ISEE Middle Level Quantitative Resources

Example Questions

Example Question #1 : Equations

Example Question #3 : How To Find The Solution To An Equation

Example Question #3 : How To Find The Solution To An Equation

Example Question #5 : How To Find The Solution To An Equation

Example Question #8 : Equations

Example Question #4 : How To Find The Solution To An Equation

Example Question #5 : How To Find The Solution To An Equation

Example Question #11 : Equations

Example Question #132 : Isee Middle Level (Grades 7 8) Quantitative Reasoning

Example Question #131 : Isee Middle Level (Grades 7 8) Quantitative Reasoning

All ISEE Middle Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: