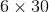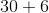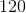ISEE Lower Level Quantitative : Equations
Study concepts, example questions & explanations for ISEE Lower Level Quantitative
All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #11 : How To Find The Solution To An Equation
Alice has 30 flowers to put in 6 different vases. Which expression represents the number of flowers in each vase?
Since there are 30 total flowers and 6 vases, we divide 30 by 6. The result is 5 flowers per vase.
Example Question #12 : How To Find The Solution To An Equation
A water bottle, basketball, and whistle all weigh a combined 5 kg. If the water bottle weighs 1 kg and the basketball weighs 3 kg, how much does the whistle weigh?
Since the total weight is 5 kg and the other two items weigh a total of 4 kg, subtract 4 from 5. Therefore the whistle weighs 1 kg.
Example Question #13 : How To Find The Solution To An Equation
Michael bought 6 bags of candy at a cost of $4 per bag. Which equation represents the amount of money he spent?
Since he bought 6 bags of candy at $4 each, we need to multiply 
Example Question #14 : How To Find The Solution To An Equation
Which of the following phrases can be written as the algebraic expression 
Eight subtracted from the quotient of a number and five
The difference of a number and eight divided by five
The difference of eight and a number divided by five
The quotient of a number and five subtracted from eight
The difference of a number and eight divided into five
Eight subtracted from the quotient of a number and five
We combine these -
Example Question #15 : How To Find The Solution To An Equation
Which of the following phrases can be written as the algebraic expression 
The quotient of seven and a number subtracted from ten
The quotient of a number and seven subtracted from ten
The difference of a number and ten divided into seven
Ten subtracted from the quotient of a number and seven
The difference of a number and ten divided by seven
The quotient of a number and seven subtracted from ten
Therefore,
Example Question #16 : How To Find The Solution To An Equation
Which of the following phrases can be written as the algebraic expression 
Nine divided into the difference of fourteen and a number
Fourteen subtracted from the quotient of a number and nine
The quotient of a number and nine subtracted from fourteen
Nine divided by the difference of a number and fourteen
Nine divided by the difference of fourteen and a number
Nine divided into the difference of fourteen and a number
Therefore,
Example Question #17 : How To Find The Solution To An Equation
Forty more than one-third of a number is eighty. What is the number?
If we let 
"Forty more than one-third of a number" can be written as
Set this equal to eighty and solve:
By the subtraction property of equality:
By the multiplication property of equality:
Example Question #18 : How To Find The Solution To An Equation
One third of the difference of a number and fifty is ninety-five. What is the number?
If we let
"One third of the difference of a number and fifty" can be written as
Set this equal to ninety-five and solve:
By the multiplication property of equality:
By the addition property of equality:
Example Question #19 : How To Find The Solution To An Equation
K is divisible by 7. 
Given that the number 49 is divisible by 7, it is a potential value of K.
Using the equation, 
Given that 52 is divisible by 26, the correct answer is 49.
Example Question #20 : How To Find The Solution To An Equation
What is the value of h in the expression below?
The steps for solving the equation, 
First, multiply 3 by the components of the parentheses.
Subtract 12 from each side.
Divide each side by 15.
Certified Tutor
Certified Tutor
All ISEE Lower Level Quantitative Resources
