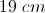All Intermediate Geometry Resources
Example Questions
Example Question #88 : Prisms
A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.
Recall how to find the volume for any prism:
First find the volume of the rectangular prism:
Next, find the volume of the triangular prism.
Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.
Recall how to find the area of an equilateral triangle:
Plug in the given side to find the area of the triangle.
Next, notice that the width of the rectangular prism is also the height of the triangular prism.
Now, find the volume of the triangular prism.
To find the volume of the entire figure, add the individual volumes together.
Make sure to round to 
Example Question #89 : Prisms
A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.
Recall how to find the volume for any prism:
First find the volume of the rectangular prism:
Next, find the volume of the triangular prism.
Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.
Recall how to find the area of an equilateral triangle:
Plug in the given side to find the area of the triangle.
Next, notice that the width of the rectangular prism is also the height of the triangular prism.
Now, find the volume of the triangular prism.
To find the volume of the entire figure, add the individual volumes together.
Make sure to round to 
Example Question #90 : Prisms
A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.
Recall how to find the volume for any prism:
First find the volume of the rectangular prism:
Next, find the volume of the triangular prism.
Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.
Recall how to find the area of an equilateral triangle:
Plug in the given side to find the area of the triangle.
Next, notice that the width of the rectangular prism is also the height of the triangular prism.
Now, find the volume of the triangular prism.
To find the volume of the entire figure, add the individual volumes together.
Make sure to round to 
Example Question #91 : Prisms
A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.
Recall how to find the volume for any prism:
First find the volume of the rectangular prism:
Next, find the volume of the triangular prism.
Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.
Recall how to find the area of an equilateral triangle:
Plug in the given side to find the area of the triangle.
Next, notice that the width of the rectangular prism is also the height of the triangular prism.
Now, find the volume of the triangular prism.
To find the volume of the entire figure, add the individual volumes together.
Make sure to round to 
Example Question #92 : Prisms
A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.
Recall how to find the volume for any prism:
First find the volume of the rectangular prism:
Next, find the volume of the triangular prism.
Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.
Recall how to find the area of an equilateral triangle:
Plug in the given side to find the area of the triangle.
Next, notice that the width of the rectangular prism is also the height of the triangular prism.
Now, find the volume of the triangular prism.
To find the volume of the entire figure, add the individual volumes together.
Make sure to round to 
Example Question #93 : Prisms
A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.
Recall how to find the volume for any prism:
First find the volume of the rectangular prism:
Next, find the volume of the triangular prism.
Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.
Recall how to find the area of an equilateral triangle:
Plug in the given side to find the area of the triangle.
Next, notice that the width of the rectangular prism is also the height of the triangular prism.
Now, find the volume of the triangular prism.
To find the volume of the entire figure, add the individual volumes together.
Make sure to round to 
Example Question #94 : Prisms
A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base, as shown by the figure below.

Find the volume of the figure.

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.
Recall how to find the volume for any prism:
First find the volume of the rectangular prism:
Next, find the volume of the triangular prism.
Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.
Recall how to find the area of an equilateral triangle:
Plug in the given side to find the area of the triangle.
Next, notice that the width of the rectangular prism is also the height of the triangular prism.
Now, find the volume of the triangular prism.
To find the volume of the entire figure, add the individual volumes together.
Make sure to round to 
Example Question #221 : Solid Geometry

The above figure shows a square pyramid inscribed inside a cube. The pyramid has volume 100. Give the volume of the cube.
Let 


The volume of a pyramid is one third the product of its height and the area of its base. The height of the pyramid is 
The volume of the cube is 
or, equivalently,
That is, the volume of the cube is three times that of the pyramid, and, since the pyramid has volume 100, the volume of the cube is 
Example Question #71 : Solid Geometry
A rectangular box has two sides with the following lengths:

If it possesses a volume of 
16
12
21
28
49
28
The volume of a rectangular prism is found using the following formula:
If we substitute our known values, then we can solve for the missing side.
Divide both sides of the equation by 12.
We now know that the missing length equals 7 centimeters.
This means that the box can have sides with the following dimensions: 3cm by 4cm; 7cm by 3cm; or 7cm by 4cm. The greatest area of one side belongs to the one that is 7cm by 4cm.
Example Question #1 : How To Find The Diagonal Of A Prism
What is the length of the diagonal of a rectangular box with the dimensions of 
To solve this problem we need an extension of the Pythagorean Theorem:
So the equation to solve becomes
So the distance of the diagonal is 
Certified Tutor
Certified Tutor
All Intermediate Geometry Resources