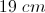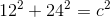We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Prisms

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #224 : Solid Geometry

A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

Possible Answers:

697.03

741.48

702.18

731.29

Correct answer:

702.18

Explanation:

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.

Recall how to find the volume for any prism:

$\text{Volume of Prism}=\text{Area of base}\times \text{height}$

First find the volume of the rectangular prism:

$\text{Volume of Rectangular Prism}=(7)(7)(10)=490$

Next, find the volume of the triangular prism.

Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.

Recall how to find the area of an equilateral triangle:

$\text{Area of Equilateral Triangle}=\frac{\sqrt3}{4}(\text{side})^2$

Plug in the given side to find the area of the triangle.

$\text{Area of Equilateral Triangle}=\frac{\sqrt3}{4}(7^2)=\frac{49\sqrt3}{4}$

Next, notice that the width of the rectangular prism is also the height of the triangular prism.

Now, find the volume of the triangular prism.

$\text{Volume of Triangular Prism}=\frac{49\sqrt3}{4}(10)=\frac{490\sqrt3}{4}$

To find the volume of the entire figure, add the individual volumes together.

$\text{Volume of Figure}=\text{Volume of Rectangular Prism}+\text{Volume of Triangular Prism}$

$\text{Volume of Figure}=490+\frac{490\sqrt3}{4}=702.18$

Make sure to round to places after the decimal.

Report an Error

Example Question #91 : Prisms

A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

Possible Answers:

1115.27

1295.67

1236.09

1276.81

Correct answer:

1276.81

Explanation:

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.

Recall how to find the volume for any prism:

$\text{Volume of Prism}=\text{Area of base}\times \text{height}$

First find the volume of the rectangular prism:

$\text{Volume of Rectangular Prism}=(9)(9)(11)=891$

Next, find the volume of the triangular prism.

Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.

Recall how to find the area of an equilateral triangle:

$\text{Area of Equilateral Triangle}=\frac{\sqrt3}{4}(\text{side})^2$

Plug in the given side to find the area of the triangle.

$\text{Area of Equilateral Triangle}=\frac{\sqrt3}{4}(9^2)=\frac{81\sqrt3}{4}$

Next, notice that the width of the rectangular prism is also the height of the triangular prism.

Now, find the volume of the triangular prism.

$\text{Volume of Triangular Prism}=\frac{81\sqrt3}{4}(11)=\frac{891\sqrt3}{4}$

To find the volume of the entire figure, add the individual volumes together.

$\text{Volume of Figure}=\text{Volume of Rectangular Prism}+\text{Volume of Triangular Prism}$

$\text{Volume of Figure}=891+\frac{891\sqrt3}{4}=1276.81$

Make sure to round to places after the decimal.

Report an Error

Example Question #92 : Prisms

A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base as shown by the figure below.

Find the volume of the figure.

Possible Answers:

58445.67

53737.98

59747.38

63838.92

Correct answer:

53737.98

Explanation:

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.

Recall how to find the volume for any prism:

$\text{Volume of Prism}=\text{Area of base}\times \text{height}$

First find the volume of the rectangular prism:

$\text{Volume of Rectangular Prism}=(25)(25)(60)=37500$

Next, find the volume of the triangular prism.

Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.

Recall how to find the area of an equilateral triangle:

$\text{Area of Equilateral Triangle}=\frac{\sqrt3}{4}(\text{side})^2$

Plug in the given side to find the area of the triangle.

$\text{Area of Equilateral Triangle}=\frac{\sqrt3}{25}(7^2)=\frac{625\sqrt3}{4}$

Next, notice that the width of the rectangular prism is also the height of the triangular prism.

Now, find the volume of the triangular prism.

$\text{Volume of Triangular Prism}=\frac{625\sqrt3}{4}(60)=9375\sqrt3$

To find the volume of the entire figure, add the individual volumes together.

$\text{Volume of Figure}=\text{Volume of Rectangular Prism}+\text{Volume of Triangular Prism}$

$\text{Volume of Figure}=37500+9375\sqrt3=53737.98$

Make sure to round to places after the decimal.

Report an Error

Example Question #93 : Prisms

A triangular prism with an equilateral triangle base is placed on top of a rectangular prism with a square base, as shown by the figure below.

Find the volume of the figure.

Possible Answers:

926.38

930.88

1909.06

1834.26

Correct answer:

1834.26

Explanation:

In order to find the volume of the figure, we will first need to find the volume of the rectangular and triangular prisms.

Recall how to find the volume for any prism:

$\text{Volume of Prism}=\text{Area of base}\times \text{height}$

First find the volume of the rectangular prism:

$\text{Volume of Rectangular Prism}=(8)(8)(20)=1280$

Next, find the volume of the triangular prism.

Notice that the length of the rectangular prism is the same as the side of the equilateral triangle that makes up one of the bases of the triangular prism.

Recall how to find the area of an equilateral triangle:

$\text{Area of Equilateral Triangle}=\frac{\sqrt3}{4}(\text{side})^2$

Plug in the given side to find the area of the triangle.

$\text{Area of Equilateral Triangle}=\frac{\sqrt3}{4}(8^2)=16\sqrt3$

Next, notice that the width of the rectangular prism is also the height of the triangular prism.

Now, find the volume of the triangular prism.

$\text{Volume of Triangular Prism}=16\sqrt3(10)=160\sqrt3$

To find the volume of the entire figure, add the individual volumes together.

$\text{Volume of Figure}=\text{Volume of Rectangular Prism}+\text{Volume of Triangular Prism}$

$\text{Volume of Figure}=1280+160\sqrt3=1834.26$

Make sure to round to places after the decimal.

Report an Error

Example Question #94 : Prisms

Pyramid

The above figure shows a square pyramid inscribed inside a cube. The pyramid has volume 100. Give the volume of the cube.

Possible Answers:

200

300

$233\frac{1}{3}$

$333\frac{1}{3}$

250

Correct answer:

300

Explanation:

Let be the length of one side of the cube. Then the base of the pyramid is a square with sidelength , and its area is

$B = s^{2}$ .

The volume of a pyramid is one third the product of its height and the area of its base. The height of the pyramid is , so the volume is

$V_{1} = \frac{1}{3} Bh = \frac{1}{3} s^{2} \cdot s = \frac{1}{3} s^{3}$

The volume of the cube is $V_{2} = s^{3}$ , so

$V_{1} = \frac{1}{3} V_{2}$

or, equivalently,

$3 \cdot V_{1} =3 \cdot \frac{1}{3} V_{2}$

$V_{2} = 3 \cdot V_{1}$

That is, the volume of the cube is three times that of the pyramid, and, since the pyramid has volume 100, the volume of the cube is $3 \cdot 100 =300$ .

Report an Error

Example Question #1 : How To Find The Volume Of A Prism

A rectangular box has two sides with the following lengths:

3$ cm$ and 4 $ cm$

If it possesses a volume of $84$ cm$^{3}$ , what is the area of its largest side?

Possible Answers:

Correct answer:

Explanation:

The volume of a rectangular prism is found using the following formula:

$V=l\times w\times h$

If we substitute our known values, then we can solve for the missing side.

$84=3\times 4\times x$

84=12x

Divide both sides of the equation by 12.

$\frac{84}{12}=\frac{12x}{12}$

x=7

We now know that the missing length equals 7 centimeters.

This means that the box can have sides with the following dimensions: 3cm by 4cm; 7cm by 3cm; or 7cm by 4cm. The greatest area of one side belongs to the one that is 7cm by 4cm.

$A=l\times w$

$A=4\times 7$

A=28

Report an Error

Example Question #1 : How To Find The Diagonal Of A Prism

What is the length of the diagonal of a rectangular box with the dimensions of $3\; cm\times 4\; cm\times 12 \; cm$ ?

Possible Answers:

$19\; cm$

$13\; cm$

$17\; cm$

$15\; cm$

$11\; cm$

Correct answer:

$13\; cm$

Explanation:

To solve this problem we need an extension of the Pythagorean Theorem:

$d^{2}=x^{2}+y^{2}+z^{2}$

So the equation to solve becomes $d^{2}=3^{2}+4^{2}+12^{2}=9+16+144=169$

So the distance of the diagonal is $13\; cm$ .

Report an Error

Example Question #1 : How To Find The Diagonal Of A Prism

Find the diagonal of the prism. The diagonal is represented by the dashed line.

Find_the_diagonal

Possible Answers:

12√5

31.2

$8\sqrt{13}$

Correct answer:

31.2

Explanation:

The length of the diagonal is from the bottom left hand corner closest to us to the top right hand corner that's farthest away from us.

This kind of a problem may seem to be a little more complicated than it really is.

In order to solve for the diagonal length, all that's required is the Pythagorean Theorem. This equation will be used twice to solve for the dashed line.

For the first step of this problem, it's helpful to imagine a triangle "slice" that's being taken inside the prism.

Find_the_diagonal_resolution , where the diagonal of interest is D2, and D1 is the diagonal that cuts from corner to corner of the bottom face of the prism. Of this triangle that's outlined in pink dashed lines, the given information (the dimensions of the prism) provides a length for one of the legs (16).

We can already "map out" that D2 (the hypotenuse of the dashed triangle) can be solved by using the Pythagorean Theorem if we can obtain the length of the other leg (D1).

The next step of this problem is to solve for D1. This will be the first use of the Pythagorean theorem. D1 is the diagonal of the base and is limited to a 2D face. This can be represented as:

Find_the_diagonal_resolution_2

The hypotenuse of the base, or the mystery length leg of the dashed triangle, can be solved by using the Pythagorean Theorem:

a^2+b^2=c^2

12^2+24^2=c^2

144+576=c^2

720=c^2

$\sqrt{720}=\sqrt{c^2}$

$\sqrt{720}=c$

${c=12\sqrt{}5}{= D1}$

Now that we calculated the length of D1, D2 can be solved for by using the Pythagorean Theorem a second time:

a^2+b^2=c^2

$16^2+(12\sqrt{5})^2=c^2$

256+720=c^2

976=c^2

$\sqrt{976}=\sqrt{c^2 }$

$\sqrt{976}=c$

${4\sqrt{61}=c \approx 31.2=D2}$

Report an Error

Example Question #1 : How To Find The Diagonal Of A Prism

A right rectangular prism has a width of cm, a length of cm, and a height of cm. Find the diagonal distance of the prism.

Possible Answers:

$2\sqrt{42} cm$

$4\sqrt{42} cm$

$\sqrt{168} cm$

$2\sqrt{5} cm$

None of the other answers.

Correct answer:

$2\sqrt{42} cm$

Explanation:

To find the diagonal distance of a prism, you can use the formula:

$d = \sqrt{w^{2} + l^{2} + h^{2}}$ , where = height; = width, and = length.

So, in this problem

$d = \sqrt{2^{2} + 8^{2} + 10^{2} } = \sqrt{4 + 64 + 100} = \sqrt{168} = \sqrt{4 * 42} = 2\sqrt{42}$ .

Report an Error

Example Question #2 : How To Find The Diagonal Of A Prism

A right rectangular prism has a height of ft, a width of feet and a length that is twice its width. The volume of the prism is cubic feet. What is the diagonal of the prism?

Possible Answers:

49 ft.

7 ft.

$\sqrt{22} ft.$

None of the other answers.

6 ft.

Correct answer:

7 ft.

Explanation:

First, given the volume, you need to find the width and length. The volume of a right, rectangular prism can be found using

V = lwh , so $36 = 2x \cdot x \cdot 2$ , where represents the length and represents the width.

Solving for , you get

$36 = 2x^{2} \cdot 2, 18 = 2x^{2}, 9 = x^{2}, 3 = x.$

So, the width of the prism is 3 feet.

Remember that the length is twice the width, so the length is 6 feet.

Now you may use the formula for finding the diagonal:

$d = \sqrt{l^{2} + w^{2} + h^{2}}$ . So, $d = \sqrt{6^{2} + 3^{2} + 2^{2}} = \sqrt{36 + 9 + 4} = \sqrt{49} = 7$ .

Report an Error

View Tutors

Kaylee
Certified Tutor

Brigham Young University, Bachelor, MFA - Animation.

View Tutors

Angela
Certified Tutor

North Georgia College State University, Bachelor of Science, Special Education. North Georgia College State University, Mas...

View Tutors

Dereika
Certified Tutor

Southern University and A & M College, Bachelor of Science, Accounting. Grand Canyon University, Master of Science, Accounting.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Washington DC, Statistics Tutors in Los Angeles, Physics Tutors in Dallas Fort Worth, Biology Tutors in Denver, Spanish Tutors in New York City, French Tutors in Denver, Physics Tutors in Denver, SSAT Tutors in Boston, Computer Science Tutors in Philadelphia, SAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Miami, LSAT Courses & Classes in Washington DC, Spanish Courses & Classes in Los Angeles, SSAT Courses & Classes in Seattle, SAT Courses & Classes in Miami, Spanish Courses & Classes in Philadelphia, Spanish Courses & Classes in Denver, Spanish Courses & Classes in Houston, MCAT Courses & Classes in New York City

Popular Test Prep

ISEE Test Prep in Dallas Fort Worth, SAT Test Prep in Dallas Fort Worth, ACT Test Prep in San Diego, SAT Test Prep in Houston, GMAT Test Prep in Phoenix, GRE Test Prep in New York City, SSAT Test Prep in Philadelphia, SAT Test Prep in Washington DC, LSAT Test Prep in New York City, SSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Prisms

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #224 : Solid Geometry

Example Question #91 : Prisms

Example Question #92 : Prisms

Example Question #93 : Prisms

Example Question #94 : Prisms

Example Question #1 : How To Find The Volume Of A Prism

Example Question #1 : How To Find The Diagonal Of A Prism

Example Question #1 : How To Find The Diagonal Of A Prism

Example Question #1 : How To Find The Diagonal Of A Prism

Example Question #2 : How To Find The Diagonal Of A Prism

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: